Las preguntas anteriores, al menos la primera de ellas, son muy conocidas. Si la habéis oído alguna vez habréis reconocido la pregunta de " ¿soporta un avión el peso de un pájaro que está volando dentro de él?". Siento que el formularla mencionando al monje que transporta pájaros sea un poco artificial, pero yo no hago más que recoger hechos verídicos que ocurrieron en la montaña de los monjes.
Las respuestas están divididas en dos partes. En la primera de ellas hay una explicación sencilla, pero es una a la que podrían ponerse pegas. En la segunda he intentado dar la misma respuesta de una forma más precisa. Un hecho curioso es que las respuestas a las dos preguntas están muy relacionadas, cosa que puede no resultar clara a primera vista y que resulta más evidente tras leer la segunda explicación.
La respuesta simple
No se puede cruzar el puente de ninguna de las dos formas, salvo bajo algunas condiciones un tanto extrañas de las que hablaremos luego. Esto no es nada sorprendente, porque de lo contrario en la realidad alguien habría inventado un método sencillo basado en esto para transportar cosas, por ejemplo en avión, con menos esfuerzo, y los recargos por sobrepeso en los vuelos serían cosa del pasado.
Empecemos con el explorador y sus pájaros.
Si un objeto está cerca de la Tierra, ésta ejerce siempre la misma fuerza sobre él sin importar dónde esté, ya sea en el agua, dentro de una caja o en el suelo, (ignorando algunas diferencias mínimas, como las que se dan según la altura) y los pájaros no son ninguna excepción. Si no acaban cayendo es porque hay algo que ejerce una fuerza sobre ellos que contrarresta la de la gravedad.
Además, se cumple el principio de acción y reacción: si hay una cierta fuerza de una cosa sobre otra en un sentido, tiene que haber otra fuerza de esta última cosa sobre la primera igual y en sentido contrario. Si un pájaro se mantiene en el aire, hay una fuerza que impide que se caiga, y tiene que haber otra fuerza en sentido contrario sobre algo en lo que el pájaro se apoye. En el caso del pájaro, para no caer debe "apoyarse", ejercer un fuerza, sobre el aire dentro de la caja, y de la misma forma el aire debe hacer fuerza sobre la caja, así que el peso completo del pájaro al final recae sobre la caja.
En una caja cerrada no importa que los pájaros vuelen, salten o se muevan de un sitio a otro. Pueden sacudir la caja, hacer que durante un momento aparente pesar más o menos; sin embargo, el peso medio que debe soportar el explorador es el mismo. Si en cierto momento es un poco menos, después será un poco más, de forma que el método no sirve para cruzar el puente.
En cuanto al monje, para lanzar las sandías al aire debe empujarlas hacia arriba, con lo que necesitará ejercer más fuerza sobre el puente que la necesaria para simplemente sostener la sandía. De la misma forma, cuando las sandías caen llevan cierta velocidad y el monje debe hacer fuerza sobre ellas para pararlas, y esta fuerza se transmite al puente. El resultado final es que haga como haga el monje malabarismos alguna vez tendrá que hacer la fuerza que sería necesaria (o más) para sostener las tres sandías a la vez, así que el método tampoco le será útil.
¿Y si el monje inventase algún ingenioso procedimiento para lanzar y recoger las sandías? ¿Y si las lanzase y parase con mucho, mucho cuidado, de forma que casi no aumentase la fuerza que debe hacer sobre el puente? Y si los pájaros se están moviendo todo el rato arriba y abajo, ¿podemos decir que algo está soportando su peso?. Muchas de las respuestas recibidas dicen que no puede lanzar las sandías porque al lanzar una de ellas al aire la fuerza que debe hacer es el doble de su peso. ¡No tiene por qué ser el doble!. Debe ser más, sí, pero tal vez sólo un poco más de cuatro kilos, digamos cinco. Si siempre hay una en el aire esto no se pasa del límite. ¿Cómo sabemos que alguna vez tiene que empujar una con más fuerza de la que se puede permitir?
En realidad, tanto esta respuesta como la anterior se deducen de un principio general sobre el que podéis leer a continuación, que no depende de si el monje es capaz o no de hacer malabarismos con una sóla mano o de lanzar las sandías a diez metros de altura, o los pájaros se mueven arriba y abajo. El razonamiento anterior es correcto, no tiene nada de malo, pero no es completo en el sentido de que no puede contestar a preguntas como las que acabo de hacer. El que viene ahora es completo, pero tal vez es algo más difícil de entender.
La respuesta larga
Si los pájaros se mantienen a la misma altura, tal vez la ley de acción y reacción es una respuesta suficientemente precisa. Pero si uno piensa en sandías que se lanzan al aire, ¿cómo sabemos que la fuerza necesaria para lanzar las sandías hace que se caiga el puente? ¿No podría ser un poco menos? Y si pensamos más detenidamente en el pájaro, éste debe empujar las moléculas del aire hacia abajo para mantenerse, y tal vez este aire tarde un poco en empujar el fondo de la caja, mientras choca con otras moléculas, y luego con otras más. La ley de acción y reacción habla de fuerzas que se ejercen en el mismo momento, no de qué pasa entre un choque y el siguiente. ¿De verdad sigue siendo válido lo anterior? El aire no es un objeto sólido. ¿Es que tal ley sirve también para cosas como gases y líquidos? ¿y si en algunos casos, con todos esos choques entre moléculas, se pierde un poco del peso inicial? ¿no habría que estudiar cómo chocan para ver si de verdad el peso sigue siendo el mismo?.
La explicación precisa de las respuestas anteriores, que da cuenta de estas preguntas, no es completamente evidente. Se basa en el siguiente principio general:
"El centro de masas de un sistema se mueve igual que si la resultante de las fuerzas exteriores estuviera aplicada a la masa total del sistema concentrada en su centro de masas"
Éste, o similar, es el enunciado que suele aparecer en los libros de física. En concreto, éste está tomado del libro de Herbert Goldstein, Mecánica Clásica (Ed. Reverté, 1998). Explicaremos con detalle su significado.
¿A qué nos referimos con eso de "un sistema"?
Aquí, un sistema es simplemente una parte del mundo. Una mesa es un sistema. La mitad de una mesa es también otro sistema, aunque la mesa no esté separada de su otra mitad. Una caja con pájaros dentro es un sistema. La Tierra es un sistema; la Tierra y la Luna forman otro sistema. Aquí, la palabra "sistema" es muy general.
¿Qué son fuerzas "exteriores" a un sistema?
Bueno... son fuerzas provocadas por partes del mundo que no están dentro del sistema. Si consideramos a la Tierra como un sistema, la fuerza gravitatoria que ejerce sobre ella el Sol es una fuerza externa. Si consideramos como sistema al Sol y a la Tierra, esta misma fuerza es una fuerza interna.
En cuanto al significado de "fuerza", basta decir que nos será suficiente con su significado común.
¿Y el centro de masas?
Es un punto del espacio que representa una especie de media de las posiciones y las masas de los trozos que forman el sistema. Si pensamos, por ejemplo, en una pelota de tenis, su centro de masas está precisamente en su centro, en el interior de la pelota. Si pensamos en dos naranjas separadas por un metro, su centro de masas está a medio metro de cada una de ellas. En cuanto a la Tierra y la Luna, su centro de masas está en la línea que las une, más cerca del centro de la Tierra que de la Luna, ya que la Tierra es mayor y tiene más masa (de hecho, está tan cerca que está dentro de la Tierra). El centro de masas de una cosa plana está en el punto donde podrías equilibrarla sobre la punta de un lápiz.
En la última sección puedes encontrar definiciones precisas de lo que es en realidad el centro de masas. Para comprender la explicación siguiente sólo necesitas saber que es algo que depende de la masa y la posición de las partes del sistema, que en casos comunes está más o menos cerca de su centro, en el significado usual de la palabra, y que está más cerca de las partes con más masa del sistema que de las que tienen menos masa (como en el caso de la Tierra y la Luna).
¿Y la fuerza resultante?
Es la suma de todas las fuerzas a las que se refiera, en este caso todas las fuerzas exteriores (suma como vectores). En lugar de "la resultante de todas las fuerzas exteriores" puedes leer "el efecto de todas las fuerzas exteriores" y el significado es esencialmente el mismo.
Qué dice este principio sobre los pájaros dentro de la caja
Pensemos en el explorador con su caja y todo su contenido como un sistema. Al empezar a cruzar el puente y al terminar, el centro de masas del explorador con su caja, los pájaros y el aire está más o menos a la misma altura, así que la fuerza vertical externa mientras cruzaba el puente ha tenido que ser, en media, cero, por el principio anterior. Las únicas fuerzas externas aquí son la fuerza que ejerce el puente sobre el sistema (el explorador y su caja con los pájaros) y la gravedad. Esto quiere decir que si el explorador cruza, la fuerza del puente, en media, ha tenido que ser igual a la fuerza de la gravedad sobre el explorador, su caja y los pájaros. Tened en cuenta que la fuerza de la gravedad sobre el sistema, lo que comúnmente llamamos su peso, es siempre la misma. A la Tierra no le importa si algo se mueve o salta o está metido en una caja: siempre ejerce la misma fuerza sobre ese algo.
Esta explicación, que sólo depende de que se cumplan las leyes de Newton, es en realidad la misma que la respuesta simple, un tanto disfrazada: el motivo de que se cumpla este principio es, después de todo, la ley de acción y reacción. Podéis ver los detalles de esto en la última sección.
¿Pero la fuerza sobre el puente es siempre la misma, sin importar cómo se muevan los pájaros o el explorador?
No. Está claro que si el explorador sin caja ni nada da un salto en mitad del puente, probablemente podría romperlo. Lo anterior dice que la fuerza, en media, no cambia (si a veces es más, a veces debe ser menos). En otro puente más resistente, la fuerza extra que soporta cuando el explorador salta junto con la fuerza que soporta cuando vuelve a caer se compensan exactamente con el alivio de peso del puente mientras el explorador está en el aire. Lo importante es que esto son detalles; el principio general nos dice que debe pasar, sin importar de qué forma concreta.
Qué dice este principio sobre el monje y las sandías
A estas alturas ya imagináis la respuesta al monje cruzando el puente mientras hace malabarismos: si el sistema es él con sus sandías, la fuerza que debe ejercer el puente sobre él es de nuevo, en media, la misma que si no hiciera malabarismos, así que no tiene nada que hacer. El puente se caerá en un momento u otro por culpa del peso. El lanzar la sandía y el recogerla compensan el hecho de que haya una sandía en el aire y no se consigue nada. El razonamiento anterior muestra que, de verdad, se tienen que compensar, y que esto no depende de la forma en que se lleven las sandías.
Excepciones
Todo "más o menos" tiene pequeñas escapatorias, y esta explicación no es una excepción. El enunciado tenía cierto margen, así que puede uno pensar en formas de saltarse lo anterior. Desde luego, ninguno de estos cumple las condiciones que hemos supuesto ciertas en las explicaciones anteriores.
Por ejemplo, el monje puede simplemente lanzar una de las sandías al otro lado del puente y luego pasar él. O lo que es lo mismo, puede ir corriendo y justo antes de pisar el puente lanzar una sandía muy alto, de forma que mientras él cruza el puente la sandía esté siempre directamente sobre su cabeza, pero sin que él la toque (de esta forma, están cruzando el puente "a la vez"). Si al principio el monje puede ir lo suficientemente rápido y lanzar la sandía lo suficientemente alto, entonces puede cruzar el puente, aunque la mayoría estará de acuerdo en que, de alguna forma, así se ha saltado las reglas del juego: en el enunciado se hablaba de un puente "largo". En el razonamiento de antes hemos usado que la posición vertical al principio y al final del puente era "más o menos la misma", cosa que no pasa en este caso.
El explorador podría conseguir una caja muy, muy alta, y atar los pájaros al techo de dicha caja con una cuerdecilla. Justo al entrar en el puente, el explorador suelta la cuerdecilla y cruza tranquilamente mientras los pájaros caen en caída libre y no ejercen ninguna fuerza sobre el puente.
Desde luego, esto es muy parecido a simplemente lanzar los pájaros al otro lado.
Estos métodos, posibles en teoría, tienen en común el hecho de que el centro de masas del caminante con su carga experimenta siempre una aceleración hacia abajo mientras cruzan el puente, ya que se puede esperar que el puente contrarreste totalmente la gravedad. Cualquier método que sea posible inventar cumple esto, y teniéndolo en cuenta sería posible calcular cuál es la longitud máxima del puente que podrían cruzar, y a qué velocidad deberían ir al principio para cruzarlo. Y desde luego, aquí sólo tenemos en cuenta los métodos en los que los efectos importantes estén dentro de la mecánica clásica.
Objeciones a la explicación anterior
"En el caso de los pájaros no puede aplicarse la mecánica clásica, ya que se pierde energía cuando los pájaros baten las alas, y se disipa en forma de calor antes de que el aire ejerza fuerza en el suelo de la caja o en otro lugar. Aquí las fuerzas no son conservativas."
Esa disipación de energía en forma de calor debe ocurrir, pero entra dentro de la mecánica clásica. En ésta la pérdida de energía en forma de calor se entiende como el aumento de la energía cinética de las partículas, esto es, de la velocidad con que se mueven, y no hay nada que nos impida aplicarle el razonamiento que hemos hecho, que además no depende en absoluto de que las fuerzas que actúen sean o no conservativas o de dónde vengan. El principio es cierto para fuerzas que cumplan las tres leyes de Newton, sin más.
"¿Y si los pájaros están en una jaula con barrotes en lugar de una caja cerrada?"
Bueno, en ese caso es verdad que no podemos seguir el mismo razonamiento. Falla porque las fuerzas externas son posiblemente otras: masas de aire que empujan a los pájaros sosteniéndolos, por ejemplo. Falla también la parte en la que se dice "al empezar a cruzar el puente y al terminar, el centro de masas del explorador con su caja, los pájaros y el aire está más o menos a la misma altura". El sistema que consideramos incluye el aire que hay dentro de la caja cuando el explorador comienza a cruzar el puente, y quién sabe dónde está ese aire cuando los pájaros vuelan un rato dentro de una jaula abierta. Eso cambia el centro de masas, que ya no tiene por qué estar a la misma altura al principio y al final. Ahora ni siquiera sabemos dónde estará el sistema al acabar de cruzar el puente ni por dónde andará su centro de masas. Los pájaros podrían volar de forma que el aire que impulsan hacia abajo se saliera por los lados de la jaula en lugar de tocar su fondo. Sin embargo, es importante notar que el principio general sigue siendo cierto: esté donde esté su centro de masas, se mueve por el efecto de las fuerzas exteriores.
En este caso no podemos afirmar que el explorador está transportando a los pájaros. Más bien se están transportando ellos mismos, y entonces no hay mucha diferencia con el caso en que los pájaros cruzaran volando el puente ellos mismos para reunirse con el explorador en el otro lado. El hecho de que haya barrotes alrededor de los pájaros no cambia mucho la forma de transporte.
"A pesar de todo, tal vez hay efectos que la mecánica clásica no tiene en cuenta, y entonces todo esto no vale."
Puede ser. Intenta cruzar el puente haciendo malabarismos con sandías, o mejor pon pájaros o abejas volando en una caja y comprueba si pesan. Usa, por ejemplo, peces nadando dentro de una pecera, que es una situación muy parecida, o algo flotando en una olla con agua. Si lo haces verás que el peso está ahí.
Demostración del principio
Esta parte es más técnica que la anterior, aunque no requiere más matemáticas de las que se estudian comúnmente en el instituto. La incluyo porque sin ella la explicación que hemos dado requiere que uno confíe en la palabra de los libros de física cuando afirman que el principio citado es válido, y además es aquí donde está contenido el centro de argumento. Personalmente, me parece asombroso que tanta información pueda obtenerse simplemente de tres leyes fundamentales, las de Newton, y no me resisto a incluirlo aquí. Éste es un punto importante: el siguiente razonamiento habla de cosas (partículas) que cumplen las leyes de Newton, sin más supuestos.
Si tenemos un sistema formado por unas cuantas partículas, digamos n, situadas en los puntos del espacio r1, r2,... rn, con masas respectivamente m1, m2,... mn, entonces su centro de masas se define como la suma r1 m1+ r2 m2+... dividida por la masa total. Esto es:
Centro de masas: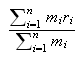 
El símbolo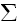 
es tan sólo una forma abreviada de escribir la suma. La masa total es 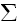mi, es decir, la suma de todas las masas m1, m2,... mn,. Normalmente (como aparece en la fórmula de arriba) se escribe debajo y encima de 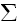una indicación sobre cuántos términos hay que sumar (en este caso, n), y qué índice es el que varía (en este caso 1). Como aquí siempre los sumaremos todos, no seguiré poniendo la n.
La segunda ley de Newton dice que la fuerza es la masa por la aceleración. Al resultado de las fuerzas externas que actúan sobre nuestra partícula número i la llamaré Fi. A la fuerza interna que ejerce la partícula i sobre la j la llamaré Fij. La aceleración de la partícula i es ai. Ocurre entonces que
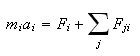
es decir, masa x aceleración = la fuerza externa + las fuerzas internas, y esto es cierto para cada partícula i. Notad que en las fuerzas internas se incluyen todas las que provocan el resto de las partículas sobre la partícula i. Podemos sumar las ecuaciones anteriores para todos los y obtener
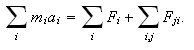
El último término es la suma de todas las fuerzas internas entre todas las partículas. La tercera ley de Newton dice que se compensan entre ellas; que para cada fuerza que haga una partícula sobre otra, recibe una fuerza igual en sentido contrario. Esto quiere decir que en este último término los sumandos se anulan de dos en dos: podemos sumarlos por parejas de una fuerza y su opuesta (Fij y Fji). Así que esa parte es cero y
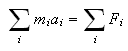
Observad que la aceleración del centro de masas es
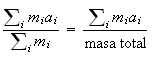
obtenida derivando dos veces respecto al tiempo. Entonces la ecuación podemos escribirla como
masa total x aceleración del centro de masas =
= la suma de las fuerzas exteriores
y esto es justamente lo que decía el principio del que hablábamos.
