Motivación
En algunos casos necesitamos más
bits aleatorios que los que pueden proporcionarnos nuestras fuentes
de entropía tal y como discutíamos en el anterior
artículo. En estos casos se recurre a los generadores de
números (o bits) pseudoaleatorios (las siglas inglesas
son PRNG= pseudo random number generator) que constituyen en definitiva
una forma de expandir unos pocos bits realmente aleatorios.
Definiciones
Un PRNG es una función que toma
cierta cantidad de verdadera aleatoriedad (llamada semilla del
generador) y genera una secuencia de bits que pueden usarse como
si fuesen auténticos números aleatorios, suponiendo
que el adversario tiene una cantidad limitada de recursos computacionales
y que la semilla es suficientemente grande como para frustrar
ataques por fuerza bruta.
La mayoría de los lenguajes de
programación (C, Pascal, BASIC, Fortran...) disponen de
funciones para generar números pseudoaleatorios que a menudo
satisfacen criterios estadísticos de aleatoriedad pero
no son suficientes para utilizar en criptografía. La razón
principal es que cuando se ve comprometido uno de los valores
inmediatamente se conocen todos los anteriores y posteriores de
la secuencia. Un PRNG criptográficamente fuerte en cambio,
es un algoritmo del que se ha probado que un oponente que conozca
el algoritmo y todos los bits generados hasta cierto punto - pero
no la semilla- no puede adivinar el siguiente bit que será
generado con probabilidad mayor que 1/2+e donde e suele decrecer
exponencialmente de acuerdo con cierto parámetro s que
típicamente sería la longitud de la semilla.
Utilización
Si se elige no usar un PRNG criptográficamente
fuerte como modo de expandir una semilla de auténticos
números aleatorios hay algunas técnicas que pueden
servir en la mayoría de los casos. La utilización
descuidada de estos métodos puede producir una reducción
catastrófica de la seguridad, en especial debemos prestar
atención a no usar una semilla demasiado pequeña
o formada por pocos bits realmente aleatorios. Por ejemplo y como
ya se hizo notar en otro sitio, la utilización -habitual-
de la fecha y hora del sistema sólo proporciona unos pocos
bits aleatorios aunque aparentemente y a través del uso
de una función hash estemos utilizando 128 o 160 bits.
Estas técnicas se resumirían
en que una función trampa enmascare algunas operaciones
fácilmente predecibles y por tanto débiles. La operación
podría consistir simplemente en contar o en el uso de un
generador de período largo. Algunas combinaciones comunes
son:
Una función hash criptográficamente
fuerte como MD5 o SHA operando sobre una semilla de auténticos
números aleatorios concatenada con un contador que se incrementa
en cada paso.
Un algoritmo de cifrado fuerte usando una clave para cifrar
una secuencia generada por un generador de periodo suficientemente
largo que ha sido inicializado con un verdadero número
aleatorio. Por ejemplo podría usarse un generador aditivo
de Marsaglia para alimentar un algoritmo triple- DES en modo
CBC.
El cifrado de un contador con una clave realmente aleatoria.
Se debe tener la precaución de usar un modo CBC y/o usar
sólo una fracción del bloque de salida, de otro
modo la secuencia de salida se reconocería como no aleatoria
al cabo de un número de bits del orden de la raíz
cuadrada del período del contador.
Presumiblemente,
predecir valores de una secuencia generada usando una de estas técnicas
equivale a romper el algoritmo de cifrado utilizado o a invertir
la función hash (que se supone no invertible). Cuanta menos
información se revele en cada iteración, tanto más
difícil será para el adversario predecir futuros valores.
Por ello a menudo se emplea un solo bit de la salida.
Resumiendo: en general un modo
correcto de uso implica empezar con una semilla fuerte, auténticamente
aleatoria, realizar uno o más pasos criptográficamente
sólidos a partir de dicha semilla y no revelar el estado
completo del generador en cada elemento de la secuencia de salida.
Naturalmente, si cada valor de la secuencia puede calcularse de
forma fija a partir del valor anterior, entonces cuando un sólo
valor de la secuencia se ve comprometido, todos los futuros valores
pueden ser determinados.
Cosas que debemos evitar
Algunos errores frecuentes para los interesados en diseñar
su propio PRNG o mejorar algunos de los ya existentes:
Sistemas caóticos: existe bastante confusión
entre lo que parece complejo para las personas y lo realmente
aleatorio.
Generadores aleatorios de las librerías matemáticas:
este tipo de generadores es apto para, por ejemplo, simulación
pero no son criptográficamente fuertes.
Generadores congruenciales lineales: los más
simples y posiblemente peores de los generadores de librería
matemática.
Chain adittion (adición en cadena) otro PRNG
que se "rompe" con facilidad.
CDROMs, CDs de audio o cintas: El material grabado
tiene un gran volumen de bits que a veces se confunde con la
aleatoriedad. Sin embargo, el número de bits necesarios
para indexar todas las grabaciones existentes en el mundo es
suficientemente pequeño como para ser adivinado por fuerza
bruta.
Usenet: de nuevo el mismo error anterior. Además
las news son públicas y accesibles por cualquier adversario.
E-mail: podría ser una fuente si estuviera
tan bien cifrado que el adversario no pueda leerlo pero nunca
estamos seguros de lo que el adversario ha visto realmente.
Para los textos ingleses utilizados como fuente de entropía,
Shannon estima un bit de entropía por carácter
como máximo.
Algunos ejemplos de PRNG
El generador lineal congruencial
Ponemos como ejemplo este generador porque
es uno de los más difundidos siendo a la vez uno de los
más débiles y no apto para uso criptográfico.
Se utiliza en la mayoría de las funciones rand() y similares.
La forma general de es: Xi+1=(a.Xi
+ b ) mod m donde X0 sería la semilla del generador.
La salida suele ser el número Xi/m, un número
en coma flotante en el intervalo [0,1).
Algunas propiedades de estos generadores:
1.- El módulo m es una cota superior del número
de valores diferentes que puede tomar la semilla.
2.- Si Xi vuelve a tomar el valor de la semilla
inicial la secuencia se repetirá cíclicamente.
3.- Todas las secuencias producidas por este tipo de generador
si se prolongan lo suficiente (periodo) acaban en un ciclo que
se repite indefinidamente.
Un buen generador
lineal tendrá un periodo tan largo como sea posible (es decir
m). Este máximo se alcanza si y sólo si se cumplen
las tres siguientes condiciones [Knuth]
a) b es primo con m
b) a-1 es múltiplo de p para todo primo p que divida
a m
c) a-1 es múltiplo de 4 siempre que m sea múltiplo
de 4
Habitualmente se toma como m una potencia
de 2 más de 1 de modo que se puede coger por ejemplo b=1
y a un número impar.
No sólo este tipo de generador
sino todos los de tipo polinómico congruencial, es decir:
x= (anxn + ... + a1x
+ a0) mod m
son predecibles y por tanto inútiles para cualquier cifrado
serio.
El generador ANSI X9.17
Este generador esta pensado como mecanismo
para generar claves DES y vectores de inicialización, usando
triple- DES como primitiva (podría usarse otro algoritmo
de cifrado de bloques). También es ampliamente usado en
banca y otras aplicaciones.
1.- K es una clave secreta para triple DES generada de algún
modo en el momento de la inicialización. Debe ser aleatoria
y usada sólo para este generador. Es parte del estado
secreto del PRNG y nunca varía con las entradas.
2.- Cada vez que se desee una salida se hace lo siguiente a)
Ti = EK(timestamp)
b) salida[i]= EK(Ti
xor semilla[i])
c) semilla[i+1]= EK(Ti xor salida[i])
Existe una variación en Crypto++ la librería
de Wei Dai implementada como sigue:
a) Ti = EK(Ti-1
xor timestamp)
b) salida[i]= EK(Ti xor semilla[i])
c) semilla[i+1]= EK(Tii xor salida[i])
Esto supone
encriptar los 'timestamp' en modo CBC en lugar del modo ECB que
utiliza el generador X9.17 estándar. El 'timestamp' se basa
en el uso de la CPU del programa y su resolución depende
de la plataforma utilizada, por ejemplo en Linux tiene una resolución
de 0.01 segundos.
El generador de DSA
DSA (Digital Signature Standard) describe
un PRNG basado en SHA pensado para generar parámetros pseudoaleatorios
para el algoritmo de firmas DSA. Este generador permite entradas
opcionales del usuario Wi mientras se generan las claves. De otro
modo el PRNG nunca se recobraría de un estado interno comprometido.
Toda la aritmética se puede realizar en módulo 2N
donde 160<= N <= 512.
1.- El generador mantiene un estado
interno Xi que varía constantemente.
2.- El generador admite una entrada
opcional Wi, se asumirá que es cero cuando no se produzca.
3.- Cada salida se produce de la siguiente manera:
a) salida[i]= hash(Wi
+ Xi mod 2160)
b) Xi+1= Xi + salida[i] + 1 mod 2160
El generador RSAREF
Este PRNG se basa en dos operaciones:
hash con MD5 y adición módulo 2128 con un diseño
relativamente simple. Consiste en lo siguiente:
1.- Un contador de 128 bits Ci
2.- Un método de procesar entradas Xi que
hace lo siguiente
Ci+1= Ci + MD5(Xi) mod 2128
3.- Un método de producir salidas así:
a) salida[i]= MD5(Ci)
mod 2128
b) Ci+1= Ci+1 mod 2128
El generador de Cryptolib
Cryptolib es una librería criptográfica
desarrollada por Lacy, Mitchell, Schnell y Blaze. La fuente principal
de aleatoriedad de esta librería es TrueRand un mecanismo
para extraer valores presumiblemente impredecibles a partir de
los sesgos existentes entre diferentes relojes del sistema. Estos
valores pueden ser utilizados directamente (no se recomienda utilizar
más de 16 bits de cada palabra de 32) o ser usados para
alimentar los dos PRNG disponibles: fsrRand y desRand.
fsrRand posee un estado secreto consistente en una
clave DES que llamaremos K y un array de siete valores de 32
bits, X0... X6, organizados como un registro
de desplazamiento (shift register). Cada vez que se requiere
una salida, dos de los valores de 32 bits se concatenan formando
un número de 64 bits. Este número se cifra con
DES usando K. El resultado se divide en dos mitades de 32 bits,
se realiza un XOR con una de ellas y uno de los valores de 32
bits modificando así uno de los registros, mientras que
la otra mitad es la salida del algoritmo. Se desplaza entonces
el registro de modo que se utilizan dos nuevos valores cada
vez que se produce una nueva salida.
desRand posee un estado secreto consistente en un
contador C de 64 bits, una clave secreta de triple DES que llamamos
K un prefijo secreto de 20 bits, P, y un sufijo secreto de 20
bits, S. Cada nueva salida de 32 bits se produce de la siguiente
manera:
1.- Usar la función hash SHA1 para calcular hash(P,C,S)
2.- Con triple- DES se calcula EK(C)
3.- Se hace un XOR de los bits de mayor peso del valor hash
con el resultado del cifrado, se ofrecen como salida los cuatro
bytes de mayor peso de dicho número.
4.- C=C+1
El generador Blum Blum Shub
Este generador que suele piadosamente
abreviarse BBS es el que actualmente tiene una prueba más
sólida de fortaleza. Es también muy simple, se basa
en residuos cuadráticos y su única desventaja es
que requiere bastante cálculos en comparación con
otros generadores clásicos.
Se empieza eligiendo dos grandes primos
p y q que al ser divididos entre 4 den resto 3. Sea n el producto
de p por q. Se elige entonces un número aleatorio x primo
con n. La semilla inicial para el generador y el método
de calcular los siguientes valores de la secuencia son:
S0=x2 mod n
Si+1=Si2 mod n
Deben emplearse sólo unos pocos
bits del final de cada Si. Siempre es seguro utilizar solamente
el bit menos significativo. Si se usan no más de log2(log2
Si) de los bits de menos peso, se demuestra que predecir
bits adicionales es tan difícil como la factorización
de n, un problema tenido por intratable actualmente y base de
métodos tan sólidos como RSA.
Otro detalle interesante de este generador
es que se puede calcular directamente cualquier valor Si sin tener
que calcular los anteriores. En concreto:
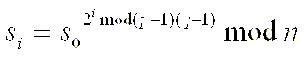
Esto significa que en aplicaciones que
generan muchas claves de esta manera, no es necesario almacenarlas
todas, cada clave puede ser reconstruida a partir de su índice
y los S y n iniciales.
Generadores de G. Marsaglia
Coge aquí
mismo una lista de generadores de números aleatorios pequeños
y listos para usarse (lenguaje C) propuestos por el gurú
George Marsaglia.
Referencias
-
Computer Generated Random Numbers,
David W. Deley
-
RFC1750, Randomness Recommendations
for Security, Estlake,Crocker & Schiller
-
Cryptoanalytic Attacks on Pseudorandom
Number Generators, Kelsey, Schneier,Wagner & Hall (www.counterpane.com)
-
Randomness resources for Dr. Dobb's
Journal readers, (www.cs.b erkeley.edu/~daw/netscape-randomness.html)
|
