Isaac Newton
Este ilustre matemático
y físico ingles nació en el año 1642 en Woolsthorpe. Al quedar
huérfano de padre y volverse a casar su madre, fue criado por
su abuela.
En 1661 al salir
de la escuela de Grantham, ingresó en el Trinity College de Cambridge,
donde en 1665 se gradúo bachiller en artes.
Durante su primer
curso en Cambridge, leyó obras de Euclides, Descartes, Kepler,
Viète y Wallis. A partir de 1663, asistió las clases que impartía
Isaac Barrow y se va familiarizando con las obras de Galileo,
Fermat, Huygens y otros. A finales de 1664, newton domina con
bastante soltura y detalle los conocimientos matemáticos de la
época y esta en condiciones de hacer sus propias contribuciones.
Durante los primeros
meses de 1665 hace sus primeros descubrimientos sobre las series
finitas y empieza a pensar en la velocidad de cambio o fluxión
de magnitudes que varían de manera continua, tales como longitudes,
áreas, distancias, etc. Estos dos tipos de problemas loa asocio
bajo el nombre de "Mi método".
Inmediatamente
después de graduarse, regresó a su casa y allí permaneció durante
todo el año 1666, ya que el Trinity College estuvo cerrado a causa
de la epidemia de peste que asoló a Inglaterra en esta época.
Este periodo lo
dedico Newton a pensar, y como consecuencia de ello conseguirá
sus principales descubrimientos: El teorema Binomial, el Cálculo,
la Ley de Gravitación universal y La naturaleza de las cosas.
En 1668 volvió
al Trinity College, del que había sido nombrado fellow el año
anterior. Allí vivirá los veintiocho años siguientes dedicado
a sus investigaciones, cuyos resultados han inmortalizado su nombre.
Cuando Barrow se
retira de la enseñanza, en 1669, a causa de ser nombrado capellán
del rey Carlos II, coopera para que nombren a Newton como sucesor
suyo en la cátedra de matemáticas.
Al ser nombrado,
Newton, gobernador de la Casa de la Moneda Británica, abandona
Cambridge en 1696 y residirá en Londres el resto de su vida.
Desde 1703 hasta
su muerte, acaecida en 1728, ocupó la presidencia del club científico
británico, La Royal Society, y en 1705 fue nombrado caballero
por la reina Ana.
Newton era poco
hablador y además le desagradaban tanto las luchas y las criticas
que se originaban inevitablemente en torno de las manifestaciones
científicas que, a causa de la controversia que originó, en 1672,
un artículo suyo publicado en la Philosophical Transactions sobre
la naturaleza de los colores, decidió no publicar nada más, hasta
que en una ocasión el astrónomo Edmund Halley fue a preguntarle
si sabía qué trayectoria seguiría un planeta alrededor del sol
suponiendo que la única fuerza que la influyera fuese una fuerza
que disminuye en relación con el cuadrado de su distancia respecto
al sol. La respuesta de Newton fue inmediata "la trayectoria
es elíptica".
Al explicar newton
todos los pormenores sobre el tema en cuestión, Halley le alentó
para que volviera a crear sus cálculos originales y los publicase.
El resultado fue la obra más influyente y revolucionaria que jamás
apareciera impresa. Newton la tituló Philosophie Naturalis Principia
Mathematica, más conocida por Los Principia. En ella no sólo explica
y razona físicamente el sistema solar, sino que también establece
las leyes de las dinámica por medio del Cálculo.
Sin embargo, ni
las instigaciones de Halley ni de Wallis pudieron convencer a
Newton para que publicase su versión de Cálculo, hasta que otro
matemático, el alemán G. W. Leibniz, 1n 1684, publica en la revista
científica Acta Eruditorum un procedimiento que había conseguido
independientemente en 1675 para el cálculo de las tangentes a
una curva cualquiera. Este procedimiento era análogo al aplicado
por Newton en 1665 para el cálculo de velocidades y aceleraciones
en movimientos variados y que le habían conducido a inventar el
cálculo.
De ahí, que si
bien la primera exposición matemática del cálculo la hace Newton
en su obra De Analysi, escrita en 1669 y publicada en 1711, su
exposición inteligible del cálculo se encuentra en la obra De
quadratura curvarum, la cual figura como anexa a otra obra titulada
La optiks, impresa en 1704.
Isaac Barrow
El precursor de
Newton en el cálculo fue su profesor Isaac Barrow, quien en 1670
publicó la obra Lectiones geometricae, en la que expone un procedimiento
para trazar una tangente a una curva, en el cual utiliza por primera
vez unas cantidades equivalentes a los términos modernos D x y
D y, Este procedimiento no lo pudo generalizar debido q que carecía
de una algoritmo universal para el binomio con exponentes enteros
y negativos, y fraccionarios.
El teorema del binomio
El teorema del
binomio nos dice que la expresión general de un binomio cualquiera,
como (x + y), elevado a la n-ésima potencia
está dada por
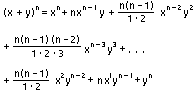
El desarrollo completo
contiene n + 1 términos, empezando con el término cero
y terminando con el término n-ésimo. En este ejemplo, el
término cero es xn. El coeficiente genérico del término
k en la expresión anterior es
=
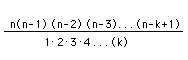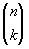
Este teorema fue desarrollado
alrededor de 1676 para exponentes fraccionarios, lo que le permitió
el uso de sus recién descubiertos métodos de cálculo para resolver
muchos problemas difíciles. El teorema del binomio, también llamado
binomio de Newton, es muy útil en varias ramas de las matemáticas,
en particular en la teoría de la probabilidad.
El método sistemático de diferenciación
Para calcular la
razón entre las velocidades instantáneas del cambio de y y de
x, o lo que es lo mismo, el cálculo de la pendiente de una curva,
Newton utilizo un procedimiento muy similar al de Barrow. Así,
por ejemplo:
Sea la curva ym
= xn, consideró a "o" un intervalo
muy pequeño, y a p y q como incrementos pequeños que experimentan
"x" e "y" durante dicho intervalo. A continuación
procedió de la forma siguiente:
Paso 1:
Si a "x"
se le da el incremento p, la "y" experimentará el incremento
q y resultaría que (y + q)m = (x + p)n.
Desarrollando ambos miembros por el teorema del binomio, queda
:
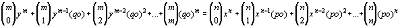
Paso 2:
Como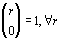 
natural se elimina los términos ym con xn,
quedando
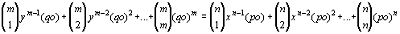
Paso 3:
Dividiendo ambos
términos por "o" y despreciando todos los términos que
todavía contengan "o" queda:
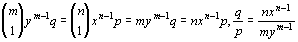
Paso 4:
Si ym = xn,
y = xn/m. Es decir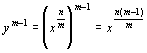 
Sustituyendo en
el resultado del paso 3 quedará
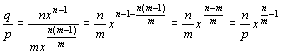
La integración como inversa
de la diferenciación
Las primeras reglas
del cálculo integral se encontraron integrando por suma directa.
Por ejemplo, si dividimos la abscisa ON=x de la figura en n partes
iguales D x =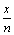 
y designamos las ordenadas correspondientes a los puntos de
división por y1, y2, …yn, la
superficie NOP limitada por la parábola y =ax2, la
ordenada extrema y el eje de las abscisas, tendrá como área aproximada:
y1D x + y2D x
+ …+ ynD x = S yi·D x.
Sustituyendo y1 por a(D
x)2, y2 por a(2D x)2, etc., tendremos
S ax2D x = aD x{(D x)2
+ (2D x)2 + (3D x)2 + …+ (n2D x)2
}= a (D x)3 {(12 + 22 + … + n2}
= a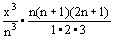 
Para n =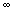 
(limite) se tendrá exactamente ò ax2dx =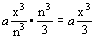 
Las dificultades
de la integración directa se encuentran en la valoración de la
suma o serie que se presenta, y para superar estas dificultades
es por lo que en general se considera a la integración como inversa
de la diferenciación.
Isaac Barrow fue
el primer hombre que se dio cuenta de que el problema de la tangente
y el problema del área son dos caras de la misma moneda. Sin embargo,
fue Newton quien primero cálculo un áreas mediante el proceso
inverso de diferenciación.
Leibniz, Gottfried Wilhelm
Leibniz, Gottfried
Wilhelm (1646-1716), también conocido como barón Gottfried Wilhelm
von Leibniz. Filósofo, matemático y estadista alemán, considerado
como uno de los mayores intelectuales del siglo XVII. Nacido en
Leipzig, se educó en las universidades de esta ciudad, de Jena
y de Altdorf. Desde 1666 (año en que fue premiado con un doctorado
en leyes) trabajó para Johann Philipp von Schönborn, arzobispo
elector de Maguncia, en diversas tareas legales, políticas y diplomáticas.
En 1673, cuando cayó el régimen del elector, Leibniz marchó a
París. Permaneció allí durante tres años y también visitó Amsterdam
y Londres, donde dedicó su tiempo al estudio de las matemáticas,
la ciencia y la filosofía. En 1676 fue designado bibliotecario
y consejero privado en la corte de Hannover. Durante los 40 años
siguientes, hasta su muerte, sirvió a Ernesto Augusto, duque de
Brunswick-Lüneburg, más tarde elector de Hannover, y a Jorge Luis,
elector de Hannover, después Jorge I, rey de Gran Bretaña.
Leibniz fue considerado
un genio universal por sus contemporáneos. Su obra aborda no sólo
problemas matemáticos y filosofía, sino también teología, derecho,
diplomacia, política, historia, filología y física.
Su primera contribución
matemática fue su tesis Desertatio de arte combinatoria, escrita
en 166, en la que expone algunas ideas sobre análisis combinatoria
y sobre la lógica formal simbólica.
En 1672 viaja a
París, en misión diplomática, y allí estudia álgebra y geometría
analítica con Huygens, quien le aconseja que si quiere ser matemático
debería leer los tratados de Pascal.
Cuando en 1673
viaja a Londres, compra las obras de Barrow, traba amistad con
algunos eruditos e incluso es muy posible que haya visto el tratado
De Analysi de Newton, en forma manuscrita.
En 1678 publica
un descubrimiento del cálculo en la revista Acta eruditorum, en
el cual pone énfasis sobre la relación inversa que hay entre la
integración y la diferenciación , así como en la importancia del
método, ya que tanto el calculus differencialis, como el calculus
sumatorius o integralis, podían ser aplicados a las curvas algebraicas
y a las no algebraicas o trascendentes.
Si bien la contribución
más importante de Leibniz a la matemática el al cálculo, no se
deben olvidar otras contribuciones menores, tale como la generalización
del teorema binomial y multimonial, la primera referencia al método
de los determinantes en occidente, algunas consideraciones sobre
le sistema de numeración binaria, gran cantidad de notaciones,
la descomposición de un numero real en términos de imaginarios,
pero sin formula para la raíces cuadradas de un numero complejo
dadas en la forma compleja. Como filosofo, afirma que no existe
una substancia única, sino pluralidad de substancias llamadas
mónadas, separadas y únicas por naturaleza, sin más relación entre
sí que la dinamante de su común procedencia del mismo Dios.
Aunque Newton llegó
mucho más allá que Leibniz en el cálculo, éste tuvo una notación
superior. Mientras Newton escribía la derivada de y como y’, la
derivada de x como x’ Leibniz las escribía dy/dx y dx/dy.
Desgraciadamente,
Newton y Leibniz, en sus últimos años mantuvieron una disputa
en torno a quien fue el primer descubridor del cálculo.
Actualmente, esta
completamente claro que a Leibniz le corresponde la primacía de
la publicación de su versión sobre el cálculo y a Newton la del
descubrimiento.
Después de haberse
encadenado dicha rivalidad, Leibniz y sus seguidores expusieron
problemas con los que esperaban dejar paradifuso a Newton. Uno
de estos problemas era el que planteo Jean Bernoulli, cuyo enunciado
consistía en hallar la fórmula de la curva sobre la cual se deslizará
una partícula, bajo la influencia de la gravedad, para moverse
desde un punto superior a otro inferior, no situados en la misma
vertical, en el menor tiempo posible. Este problema era uno d
los primeros ejemplos de máximos y mínimos. Newton lo resolvió
en una noche y llegó a la conclusión de que era la cicloide. Se
dice que al recibir la respuesta de Newton, Bernoulli manifestó
"Reconozco al león por sus garras".
Leibniz en el año
1716, el último de su vida, lo volvió a desafiar con el problema
de hallar las trayectorias ortogonales de una familia de curvas
planas. También en esa ocasión, Newton resolvió el problema y
dio un método general para hallar las trayectorias.
Guillaume de L’Hôpital
Este marqués francés
nació en París en 1661 y fue instruido en 1692, en el cálculo,
por Jean Bernoulli, quien por esas fechas residía en París.
L’Hopital pasa
a la historia de la matemática por sus obras Analisis de los infinitamente
pequeños y Tratado analítico de las secciones cónicas, que contribuían,
respectivamente, en el desarrollo del cálculo, que contribuirán,
respectivamente, en el desarrollo del cálculo y de la geometría
analítica del siglo XVIII.
La primera de las
obras mencionadas, publicadas en 1696, que contiene la obra que
conocemos hoy con el nombre de L’Hopital, en términos modernos
dice:
Si f(x) y g(x) son
funciones diferenciales en x = a tales que f(a) = g(a) = 0, entonces:
