|
Las civilizaciones de China y de la India son mucho más antiguas
que las de Grecia y Roma, aunque no más que las que surgieron en
los valles de Mesopotamia y del Nilo; ambas se remontan a la llamada
Edad Potámica, mientras que las culturas griega y romana se desarrollaron
durante la Edad Talásica. Aunque las civilizaciones que tuvieron
su cuna en las cuencas de los ríos Amarillo y Yangtze son comparables
en Edad a las que nacieron a lo largo del Nilo o entre el Eufrates
y el Tigris, los registros cronológicos en el caso de China son
mucho menos fiables que los que existen para Egipto y Babilonia.
La operación de fechar los documentos matemáticos chinos no es nada
fácil y, por ejemplo, las estimaciones que se han hecho acerca del
Chou Pei Suan Ching, considerado generalmente como el más antiguo
de los clásicos de contenido matemático, difieren entre sí en casi
mil años; el problema se complica por el hecho de que esta obra
pudiera muy bien ser debida a varios autores de diferentes épocas.
Algunos historiadores consideran el Chou Pei como un buen ejemplo
de lo que era la matemática china del 1200 a.C. aproximadamente,
pero hay otros que sitúan la obra en el primer siglo anterior a
nuestra era. Una fecha en torno al 300 a.C. podría parecer razonable,
por lo tanto, poniéndola así en estrecha competencia con otro tratado,
el Chui-chang suan-shu, escrito hacia el 250 a.C, es decir poco
antes del advenimiento de la dinastía Han (202 a.C.) Las palabras
"Chou Pei" parecen referirse al uso del gnomon para el
estudio de las órbitas circulares en los cielos, y le libro con
el mismo titulo trata, de hecho, de cálculos astronómicos, aunque
incluya también una introducción a las propiedades del triangulo
rectángulo, así como algunas cosas sobre el uso de las fracciones.
El libro esta escrito en forma de dialogo entre un principe y su
ministro sobre el calendario; el ministro explica a su soberano
que el arte de los números deriva del circulo y del cuadrado, de
los que el cuadrado pertenece a la tierra y el circulo a los cielos.
El Chou Pei nos revela que en China la geometría, tal como en Egipto,
debió surgir de la agrimensura, y que, como pasaba en Babilonia,
la geometría china se reducía a un ejercicio numérico de aritmética
y álgebra. Parece haber en él algunas indicaciones relativas al
teorema de Pitágoras, un teorema tratado, en todo caso, algebraicamente
por los chinos.
Matemática Hindú
Las matemáticas primitivas en
la India.
Las excavaciones
arqueológicas que se han desarrollado en Mohenjo Daro nos muestran
la existencia de una vieja civilización con un alto nivel cultural
en la India, contemporánea de los constructores de las grandes pirámides
egipcias, pero no ha llagado hasta nosotros ningún documento del
tipo matemático de aquella época lejana. Un milenio más tarde el
país fue ocupado por los invasores arios que procedían de las altiplanicies
del Irán, los cuales introdujeron el sistema social de castas y
desarrollaron la literatura sánscrita. Buda, el gran maestro religioso,
enseñaba en la India por época en que , según se dice, Pitágoras
visitó el país, y algunos han sugerido que quizá Pitágoras aprendió
el teorema que lleva su nombre de los hindues. Sin embargo, estudios
recientes hacen esto altamente improbable, en vista de que los babilonios
ya estaban familiarizados con el teorema en cuestión por lo menos
mil años antes.
La caída del Imperio
Romano de Occidente se sitúa tradicionalmente en el año 476, que
fue precisamente el año en que nació Aryabhata, el autor de uno
de los textos matemáticos hindues más antiguos que conocemos; esta
claro, sin embargo, que debió haber actividad de tipo matemático
en la India mucho antes de esta época, probablemente incluso antes
de la fundación mítica de Roma el 753 a.C. La India tuvo también,
como Egipto, sus ‘tensadores de cuerda’ y los conocimientos
geométricos primitivos se fueron decantando de la planificación
de templos y de la medición y construcción de altares, adoptando
la forma de un cuerpo de conocimiento conocido como los sulvasutras
o "reglas de la cuerda", La operación de extender o tensar
las cuerdas nos recuerda sorprendentemente los orígenes de la geometría
egipcia, así como su asociación con la construcción de templos y
altares nos recuerda de una manera inmediata el posible y discutido
origen ritual de la matemática. Sin embargo, la gran dificultad
que hay para atribuirle una fecha determinada a estas reglas es
solo comparable con las dudas que se plantean relativas a la influencia
que pudieron tener en los matemáticos hindues posteriores. Más aun
que en el caso de China, nos encontramos con una sorprendente falta
de continuidad de la tradición en la matemática hindú; las contribuciones
importantes son acontecimientos episódicos separados por largos
intervalos de tiempo sin ningún progreso.
Los Sulvasutras
 Se conservan tres versiones, todas ellas en verso, de la obra denominada
como los sulvasutras, la más conocida de las cuales lleva el nombre
de Apastamba. En esta exposición primitiva, que puede remontarse
quizá tan lejos en el tiempo como a la época de Pitágoras, nos encontramos
con reglas para la construcción de ángulos rectos por medios de
ternas cuyas longitudes constituyen ternas pitagóricas, tales como
son 3, 4 y 5, ó 5, 12 y 13, ó 8, 15 y 17, ó 12, 35 y 37. Sin embargo,
todas estas ternas se pueden derivar fácilmente de la vieja regla
babilónica para construirlas, y por lo tanto no es improbable que
hubiera una influencia mesopotámica en los Sulvasutras . Apastamba
sabia que el cuadrado construido sobre la diagonal de un rectángulo
es igual a la suma de los cuadrados construidos sobre dos lados
adyacentes, pero esta forma general del teorema de Pitágoras también
puedo se tomada de Mesopotamia. Más difícil de explicar es otra
de las reglas que da Apastamba, una que nos recuerda fuertemente
algunos teoremas del álgebra geométrica que aparecen en el libro
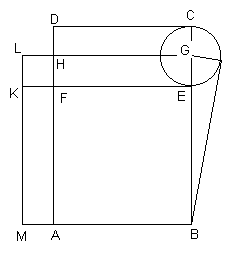
II de los Elementos de Euclides. Es la siguiente: Para construir
un cuadrado equivalente (en área) a un cuadrado ABCD dado llévense
los lados menores sobre los mayores de manera que AF=AB=BE=CD y
trácese HG mediatriz de los segmentos CE y DF; prolónguese EF hasta
K, GH hasta L y AB hasta M, de manera que FKHL=FH=AM, y trácese
la recta LKM. Constrúyase ahora un rectángulo con diagonal igual
a LG y con su lago más corto igual a HF; entonces el lado más largo
de este rectángulo es el lado x del cuadrado buscado.
Se conservan tres versiones, todas ellas en verso, de la obra denominada
como los sulvasutras, la más conocida de las cuales lleva el nombre
de Apastamba. En esta exposición primitiva, que puede remontarse
quizá tan lejos en el tiempo como a la época de Pitágoras, nos encontramos
con reglas para la construcción de ángulos rectos por medios de
ternas cuyas longitudes constituyen ternas pitagóricas, tales como
son 3, 4 y 5, ó 5, 12 y 13, ó 8, 15 y 17, ó 12, 35 y 37. Sin embargo,
todas estas ternas se pueden derivar fácilmente de la vieja regla
babilónica para construirlas, y por lo tanto no es improbable que
hubiera una influencia mesopotámica en los Sulvasutras . Apastamba
sabia que el cuadrado construido sobre la diagonal de un rectángulo
es igual a la suma de los cuadrados construidos sobre dos lados
adyacentes, pero esta forma general del teorema de Pitágoras también
puedo se tomada de Mesopotamia. Más difícil de explicar es otra
de las reglas que da Apastamba, una que nos recuerda fuertemente
algunos teoremas del álgebra geométrica que aparecen en el libro
II de los Elementos de Euclides. Es la siguiente: Para construir
un cuadrado equivalente (en área) a un cuadrado ABCD dado llévense
los lados menores sobre los mayores de manera que AF=AB=BE=CD y
trácese HG mediatriz de los segmentos CE y DF; prolónguese EF hasta
K, GH hasta L y AB hasta M, de manera que FKHL=FH=AM, y trácese
la recta LKM. Constrúyase ahora un rectángulo con diagonal igual
a LG y con su lago más corto igual a HF; entonces el lado más largo
de este rectángulo es el lado x del cuadrado buscado.
Son tan dudosos
y discutidos los orígenes y el período durante el que se desarrollaron
los Sulvasutras que no se puede decir con seguridad si estas reglas
están relacionadas o no con la primitiva agrimensura egipcia o con
el problema griego más tardío de la duplicación del altar cubico.
Los Sulvasutras han sido fechados por los historiadores de una manera
muy variada dentro de un intervalo de tiempo de casi 1000 años,
que se extiende desde el siglo VIII a.C. al siglo II de nuestra
era. La cronología local en las antiguas culturas del lejano Oriente
apenas merece ninguna confianza cuando vemos que la tradición hindú
ortodoxa se vanagloria de importantes trabajos astronómicos de hace
más de 2.000.000 de años, y cuando los cálculos conducen a billones
de días transcurridos desde el comienzo de la vida de Brahma al
400 de nuestra era aproximadamente. Las referencias en la literatura
védica a progresiones aritméticas y geométricas que pretenden remontarse
al 2000 a.C. pueden ser más seguras, probablemente, pero lo cierto
es que no hay ningún documento contemporáneo de la India que confirme
esto. También se ha pretendido que el primer reconocimiento de la
existencia de lo inconmensurable tuvo lugar en la India durante
el período de los Sulvasutras, pero tales pretensiones no están
comprobadas en absoluto. La causa a favor de un descubrimiento temprano
de las magnitudes inconmensurables por los hindues la hace de lo
más improbable el reiterado interés o incapacidad de los matemáticos
hindues para enfrentarse con los conceptos fundamentales.
Los Siddhantas
Al período
de los Sulvasutras, que se cierra hacia el siglo II de nuestra era,
le sigue la época de los Siddhantas o sistemas astronómicos. El
comienzo de la dinastía del rey Gupta (hacia el 290) señala un renacimiento
de la cultura sánscrita, y los Siddhantas parecen haber formado
parte de este renacer. Conocemos los nombres de cinco versiones
diferentes de los Siddhantas, que son el Paulisha Siddhanta, Surya
Siddhanta, Vasisishta Siddhanta, Paitamaha Siddhanta y Romanka Siddhanta.
De entre todos ellos, el Surya Siddhanta o "Sistema del Sol",
escrito hacia el año 400, parece ser el único que se conserva completo;
según el texto mismo, escrito en verso en estrofas épicas, es la
obra de Surya, el dios Sol. Las teorías astronómicas principales
son evidentemente griegas, pero aparecen mezcladas con una cantidad
considerable del viejo folklore hindú. El Paulisha Siddhanta, que
data de hacia el 380, fue resumido por el matemático hindú Varahamihira
y a él se refiere frecuentemente el sabio árabe Al-Burini, quien
le atribuye directamente o un origen o una influencia griega. Los
escritores más tardíos nos informan que todos los Siddhantas estaban
esencialmente de acuerdo en su contenido, variando sólo en la fraseología
utilizada, y así podemos suponer que los otros, al igual que el
Surya Siddhanta, eran tratados de astronomía formulados por medio
de reglas crípticas en verso sánscrito, con muy pocas demostraciones
y ninguna demostración.
Se suele admitir
que los Siddhantas aparecieron hacia finales del siglo IV o comienzos
del V, pero en lo que ya hay un marcado desacuerdo es en lo que
se refiere a los orígenes de los conocimientos que contienen. Los
historiadores hindues insisten, por supuesto, en la originalidad
y la independencia de sus autores, mientras que los escritores occidentales
se inclinan a ver en ellos signos indudables y claros de influencia
griega. Es probable, por ejemplo, que el Paulisha Siddhanta provenga
en gran parte de la obra del astrólogo Pablo, que vivió en Alejandría
poco tiempo antes de la fecha presumible en que fueron compuestos
los Siddhantas. Esta influencia vendría a explicar de una manera
natural y sencilla las obvias semejanzas que hay entre algunas partes
de los Siddhantas y la trigonometría y astronomía de Ptolomeo. El
Paulisha Siddhanta, por ejemplo, utiliza para p el valor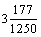 , que coincide esencialmente con el valor sexagesimal
3º8’30’’ de Ptolomeo. , que coincide esencialmente con el valor sexagesimal
3º8’30’’ de Ptolomeo.
Incluso aunque los
hindues adquiriesen sus conocimientos de trigonometría del helenismo
cosmopolita de Alejandría, el material tomó en sus manos una forma
que iba a ser muy significativa. Mientras que la trigonometría de
Ptolomeo se basaba en la relación funcional entre las cuerdas y
los correspondientes arcos o ángulos centrales en una circunferencia,
que ellas subtienden, los escritores de los Siddhantas transformaron
esto para convertirlo en un estudio de la correspondencia entre
la mitad de la cuerda y la mitad del arco o del ángulo central subtendido
por la cuerda total. Así fue como nació, aparentemente en la India,
el antepasado de la función trigonométrica moderna que conocemos
como el seno de un ángulo, y la introducción de esta función seno
representa probablemente la contribución principal de los Siddhantas
a la historia de las Matemáticas. Aunque se acepta generalmente
que este cambio de la cuerda completa a la semicuerda tuvo lugar
en la India, el historiador de la ciencia de principios de siglo
Paul Tannery formuló la hipótesis de que esta transformación de
la trigonometría pudo haber ocurrido en Alejandría durante el período
post-ptolemaico. Sea o no sea correcta esta hipótesis, lo cierto
es que el uso posterior de la semicuerda se extendió a través de
los hindues y no de los griegos, y nuestra palabra ‘seno’
se deriva del nombre hindú ‘jiva’
Aryabhata
Durante el
siglo sexto, es decir, no mucho tiempo después de la composición
de los Siddhantas, vivieron dos matemáticos hindues de los cuales
se sabe que escribieron libros sobre el mismo tipo de materias.
El más viejo y a la vez el más importante de los dos fue Aryabhata,
cuya obra más conocida, escrita hacia el 499 y titulada Aryabhatiya,
es un delgado volumen escrito en verso que cubre diversos temas
de astronomía y matemáticas. Se conocen los nombres de varios matemáticos
hindues anteriores a esta época, pero no se ha conservado nada de
sus obras, salvo unos breves fragmentos. A este respecto, pues,
la posición del Aryabhatiya es bastante análoga para el caso de
la India a la de los Elementos de Euclides para Grecia ocho siglos
antes. Las dos obras son, en efecto, recopilaciones de desarrollos
anteriores compiladas por un único autor. Y, sin embargo, hay más
diferencias, y más sorprendentes, que semejanzas entre estas dos
obras; los elementos constituyan una síntesis bien ordenada lógicamente
de la matemática pura, expuesta con un alto grado de abstracción
y con un objetivo pedagógico evidente, mientras que el Aryabhatiya
es una breve obra descriptiva escrita en 1232 estrofas métricas,
con el objeto de suplementar las reglas de cálculo utilizadas en
astronomía y en las técnicas de medición matemáticas, sin ninguna
relación con la lógica o la metodología deductiva. Una tercera parte
aproximadamente de la obre trata de ganitapada, es decir, de matemáticas;
esta sección comienza con los nombres de las potencias de diez hasta
el lugar décimo, y a continuación formula un conjunto de instrucciones
para calcular raíces cuadradas y cúbicas de números enteros. Sigue
un sistema de reglas para el cálculo de áreas, la mitad más o menos
de las cuales son erróneas; para el área de un triángulo se da la
regla correcta de calcular la mitad de producto de la base por la
altura, para el volumen de la pirámide también se toma la mitad
del producto de la base por la altura. El área de un círculo se
calcula correctamente como la mitad del producto de la circunferencia
por la mitad del diámetro, pero el volumen de la esfera viene dado
incorrectamente como el producto el área de un círculo máximo por
la raíz cuadrada de esta área. Al tratar del cálculo de áreas de
cuadriláteros aparecen de nuevo reglas correctas e incorrectas unas
al lado de las otras: el área de un trapecio viene dada por la semisuma
de los lados paralelos por la distancia perpendicular entre ellos,
y a continuación sigue la regla absurda e incomprensible de que
el área de cualquier figura plana se calcula determinando dos de
sus lados y multiplicándolos. Hay una regla en el Aryabhatiya que
señalan con orgullo los historiadores hindues de la matemática,
que es la siguient
Suma 4 a 100,
multiplica por 8 y súmale 62000. El resultado te da aproximadamente
la circunferencia de un círculo cuyo diámetro es 20000.
Aquí se puede ver
utilizado el equivalente a 3,1416 como valor de p , lo cual es ciertamente
notable, pero se debe recordar que este es el valor utilizado por
Ptolomeo. El hecho más probable es que Aryabhata estuviera influenciado
en este contexto por sus predecesores griegos viene reforzado por
su adopción de la miríada o 10000 unidades como medida del radio
de la circunferencia.
Una parte típica
del Aryabhatiya es la que trata de progresiones aritméticas, la
cual contiene reglas para calcular la suma de los términos de una
progresión, y también para hallar el número de términos de una progresión
conocido el primer término, la diferencia y la suma de todos los
términos. La primera de estas reglas había sido ya conocida mucho
antes por otros escritores, la segunda aparece formulada en una
forma tan curiosa como complicada
Multiplíquese
la suma de la progresión por ocho veces la diferencia común,
súmese el cuadrado de la diferencia entre el doble del primer
término y la diferencia común; tomese la raíz cuadrada de este
número, restese el doble del primer término, divídase por la
diferencia común, añádase uno y divídase por dos. El resultado
será igual al número de términos.
Aquí, al igual que
a todo lo largo del Araybhatiya, no se da ninguna motivación ni
justificación para esta regla. Probablemente fue obtenida resolviendo
una ecuación de segundo grado, cuyo conocimiento podría muy bien
haber venido de Mesopotamia o Grecia. A continuación da unos problemas
realmente complicados sobre interés compuesto (es decir, sobre progresiones
geométricas), el autor del libro trata, en un lenguaje muy florido,
del problema bien elemental de calcular el cuarto proporcional a
tres números dados:
En la regla
de tres multiplica el fruto por el deseo y divide por la medida.
El resultado será el fruto del deseo.
Esta es, desde luego, la regla
bien conocida que nos dice que si 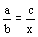 ,
entonces ,
entonces 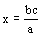 ,
donde a es ‘la medida’, b ‘el fruto’, c
‘el deseo’ y x ‘el fruto del deseo’. ,
donde a es ‘la medida’, b ‘el fruto’, c
‘el deseo’ y x ‘el fruto del deseo’.
Realmente puede
decirse que la obra de Aryabhata es un ‘popurrí’ de o
sencillo y lo complicado, a la vez que de lo correcto y lo incorrecto.
El sabio árabe Al-Biruni caracterizaba, medio milenio más tarde,
la matemática hindú como una mezcla de vulgares guijarros y valiosos
cristales, descripción que cuadra perfectamente con el Araybhatiya.
El sistema de numeración hindú
La segunda
mitad del Aryabhatiya trata de la medida y cálculo de tiempos y
de trigonometría esférica, y aquí es donde se encuentra un elemento
nuevo que iba a dejar una huella permanente en la matemática de
las generaciones futuras: el sistema de numeración posicional decimal.
No se sabe exactamente deque manera efectuaba los cálculos Aryabhata,
pero en su afirmación de que "de un lugar a otro, cada uno
es diez veces el que le precede", hay una clara indicación
de que en su mente estaba de una manera consciente la aplicación
del principio posicional. La idea de "valor local o posicional"
había sido ya un elemento absolutamente esencial del sistema de
numeración babilónico, y quizá lo que los hindues hicieron fue darse
cuenta de que esta idea era aplicable también al sistema de notación
decimal para los números enteros, que ya se estaba usando en la
India. El desarrollo histórico de las notaciones numéricas en la
India parece haber seguido más o menos los mismos pasos que en Grecia;
las inscripciones procedentes del período cultural más primitivo
de Mohenjo Daro muestran al principio un sistema consistente simplemente
en el uso de palotes verticales reunidos en grupos, pero hacia la
época de Asoka (siglo III a.C.) se usaba ya un sistema parecido
al herodiánico. En este esquema nuevo se seguía usando el principio
repetitivo, pero se adoptaron a la vez nuevos símbolos para unidades
de orden superior, concretamente para cuatro, diez, veinte y cien.
Esta manera de escribir los números, llamada escritura Karosthi,
fue evolucionando gradualmente para dar lugar a otro sistema de
notación, conocido como el de los caracteres Brahmi, que recuerda
mucho al cifrado alfabético del sistema jónico griego; cabe preguntarse,
por lo tanto, si el hecho de que el cambio tuviera lugar en la India
poco después del período durante el cual los numerales herodiánicos
se vieron desplazados por los jónicos en Gracia fue una simple coincidencia
o no.
De los numerales
cifrados del sistema Brahmi a nuestra notación moderna para los
números naturales hay que superar únicamente dos breves etapas;
la primera consiste en reconocer que utilizando estrictamente el
principio posicional, las cifras para representar los nueve primeros
números pueden servir también como cifras para los correspondientes
múltiplos de diez o, por la misma razón, como cifras para representar
los múltiplos correspondientes de cualquier potencia de diez. El
reconocer este hecho básico había convertido de golpe en superfluas
todas las cifras Brahmi, salvo las nueve primeras. No se sabe cuándo
se produjo exactamente la reducción a nueve cifras y, de hecho,
lo más probable es que la transición a la notación más ‘económica’
se hiciera de una manera gradual. Parece seguro que este importante
cambio tuvo lugar en la india, pero los orígenes de la inspiración
para llevarlo a cabo son, en cambio, poco claros. Posiblemente los
llamados numerales hindues fueran el resultado de un desarrollo
interno únicamente; quizá se desarrollaron primero en el contexto
de los intercambios occidentales de la India con Persia, en cambio,
ya que el conocimiento de la notación posicional babilónica pudo
haber conducido a una modificación del sistema Brahmi. Es posible
también que el nuevo sistema tuviera sus orígenes en los contactos
hacia en Este, con China, donde el sistema pseudoposicional de barras
pudiera haber sugerido la reducción a nueve cifras. Hay incluso
una teoría que afirma que esta reducción pudo haber tenido lugar
por primera vez en Alejandría, dentro del sistema alfabético griego,
y que esta idea debió propagarse más tarde a la India. Durante el
período alejandrino tardío, la costumbre griega de escribir las
fracciones usuales puniendo en numerados debajo del denominador
se invirtió, y ésta es precisamente la forma que adoptaron los hindues,
sin la barra que los separa. Desgraciadamente los hindues no aplicaron
el nuevo sistema de numeración para los enteros al campo de las
fracciones decimales, y así se perdió la ventaja potencial más importante
del cambio de notación de tipo jónico.
La referencia especifica
más antigua a los numerales hindues data del 662 y se encuentra
en los escritos de Severo Sebokt, un obispo sirio. Como consecuencia
del cierre de las escuelas filosóficas atenienses ordenado por Justiniano,
algunos de los sabios que enseñaban en ellas se trasladaron a Siria,
donde establecieron varios centros en los que se cultivaba el saber
griego, y Sebokt debió sentirse evidentemente molesto por el desprecio
que mostraban algunos de ellos por la cultura y por el saber no
griegos, y consideró necesario por lo tanto el recordar a aquellos
que ‘hablaban griego’ que ‘hay otros que también
saben algo’. Y para ilustrar este punto llama la atención sobre
los hindues y sus ‘sutiles descubrimientos en astronomía’
y especialmente ‘sus valiosos métodos de cálculo y sus operaciones
que sobrepasan toda descripción. Quisiera decir solamente que sus
cálculos se hacen por medio de nueve signos’. Se sabe también
que por aquella época los numerales hindues ya se habían estado
usando durante bastante tiempo.
El símbolo para el cero
Hay que hacer
notar que la referencia a nueve símbolos y no a diez implica evidentemente
que los hindues no habían superado aún la segunda etapa en la transición
hacia el sistema de numeración moderno, es decir, la que consiste
en la introducción de una notación especial para una posición que
falta o, lo que es lo mismo, de un símbolo para el cero. En la historia
de la matemática se presentan muchas situaciones anómalas, y no
es precisamente la menor la que revela el hecho de que "la
primera aparición indudable del cero en la India es en una inscripción
del año 876", es decir, más de dos siglos después de la primera
referencia conocida a los otros nueve numerales. No esta demostrado
ni siquiera que el número cero (en tanto que idea conceptualmente
distinta de un símbolo para una posición vacía) surgiera al mismo
tiempo que los otros numerales hindues. Es muy posible, en cambio,
que el cero tuviera su origen en Alejandría, y que desde allí se
propagase a la India después de que el sistema decimal posicional
se hubiera consolidado allí.
Con la introducción
del decimo numeral en el sistema de numeración hindú para representar
el cero, en la forma de un redondo huevo de oca, quedaba completo
el moderno sistema de numeración para los enteros. Aunque las formas
hindues medievales de las diez cifras numerales son muy diferentes
a las que usamos hoy en día, los principios teóricos del sistema
quedaban ya definitivamente establecidos. El nuevo sistema de numeración
que llamamos usualmente ‘sistema hindú’ no consiste más
que en una nueva combinación de tres principios básicos, todos ellos
con un origen mucha más antigua:
- Una base decimal
- Una notación posicional
- Una forma cifrada para cada uno de los diez
numerales básicos
Ninguno de estos
tres principios se debía, como se ha dicho, originalmente a los
hindues, pero lo que si se debió a ellos fue probablemente la idea
de reunir por primera vez los tres para construir el sistema de
numeración moderno.
La trigonometría hindú
El desarrollo
de nuestro sistema de notación para los números naturales fue sin
duda una de las dos contribuciones más importantes de la India en
la historia de la matemática. La otra consistió en la introducción
de lo equivalente a la función seno en trigonometría, para reemplazar
las tablas de cuerdas griegas; las tablas más antiguas de la relación
seno que han llegado hasta nosotros son las que figuran en los Siddhantas
y en el Aryabhatiya, donde se dan los senos de los ángulos menores
o iguales que 90 para 24 intervalos angulares iguales a 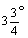 cada uno. Para expresar la longitud del arco y la del seno
en términos de la misma unidad, se tomaba como radio 3,438 unidades
y la circunferencia correspondiente como 360·60 = 21600 unidades;
estos valores implican un valor de p que coincide con el de Ptolomeo
hasta la cuarta cifra significativa, pero Aryabhata utiliza en otros
contextos el valor cada uno. Para expresar la longitud del arco y la del seno
en términos de la misma unidad, se tomaba como radio 3,438 unidades
y la circunferencia correspondiente como 360·60 = 21600 unidades;
estos valores implican un valor de p que coincide con el de Ptolomeo
hasta la cuarta cifra significativa, pero Aryabhata utiliza en otros
contextos el valor 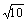 para p, valor que aparece tan frecuentemente en la India que se
le conoce a veces como ‘el valor hindú para p’
para p, valor que aparece tan frecuentemente en la India que se
le conoce a veces como ‘el valor hindú para p’
Para el seno de 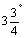 se toma exactamente el número de unidades que
contiene el arco, es decir se toma exactamente el número de unidades que
contiene el arco, es decir 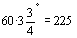 ;
traducido a lenguaje moderno, el seno de un ángulo pequeño es igual
casi igual a la medida del ángulo en radianes, que es justamente
lo que hacían los hindues. Para las entradas restantes de la tabla
de senos utilizaban una fórmula de recursión que puede expresarse
de la forma siguiente: si designamos por Sn en n-ésimo
seno en la sucesión que va de n = 1 a n = 24, y si la suma de los
n primeros senos es Rn, entonces ;
traducido a lenguaje moderno, el seno de un ángulo pequeño es igual
casi igual a la medida del ángulo en radianes, que es justamente
lo que hacían los hindues. Para las entradas restantes de la tabla
de senos utilizaban una fórmula de recursión que puede expresarse
de la forma siguiente: si designamos por Sn en n-ésimo
seno en la sucesión que va de n = 1 a n = 24, y si la suma de los
n primeros senos es Rn, entonces 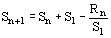 .
A partir de esta regla uno puede deducir fácilmente que sen .
A partir de esta regla uno puede deducir fácilmente que sen 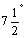 = 449, sen = 449, sen 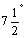 =671, sen 15º=890, y así hasta sen 90º=3438, que son los
valores que aparecen en las tablas de los Siddhantas y del Aryabhatiya.
Las tablas incluyen además los valores de lo que se conoce como
seno verso de un ángulo, es decir, de 1 – cos q en forma trigonométrica
moderna, o de 3438·(1 – cos q) en forma trigonométrica hindú,
desde sen vers. =671, sen 15º=890, y así hasta sen 90º=3438, que son los
valores que aparecen en las tablas de los Siddhantas y del Aryabhatiya.
Las tablas incluyen además los valores de lo que se conoce como
seno verso de un ángulo, es decir, de 1 – cos q en forma trigonométrica
moderna, o de 3438·(1 – cos q) en forma trigonométrica hindú,
desde sen vers. 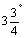 =7
a sen ves. 90º=3438. Si se divide los números que figuran en la
tabla por 3438 se encuentran resultados que se aproximan mucho a
los valores correspondientes en las tablas trigonométricas modernas. =7
a sen ves. 90º=3438. Si se divide los números que figuran en la
tabla por 3438 se encuentran resultados que se aproximan mucho a
los valores correspondientes en las tablas trigonométricas modernas.
El método de multiplicación hindú
La trigonometría
hindú fue evidentemente una herramienta para la astronomía tan útil
como precisa. El cómo llegaron los hindues a resultados tales como
la forma de recursión para los senos que se acaba de mencionar,
es desconocido, pero sí se ha sugerido que tales reglas pudieron
venir motivadas por un desarrollo intuitivo o empírico del cálculo
con ecuaciones en diferencias y de la práctica de la interpolación;
de hecho se suele caracterizar frecuentemente a la matemática hindú
en general como ‘intuitiva’, para ponerla en contraste
con el severo racionalismo griego. A pesar de que es evidente la
influencia griega en la trigonometría hindú, los hindues parecen
no haber tenido ocasión de adoptar la geometría griega, o bien no
aprovecharon la ocasión, interesados como estaban únicamente en
reglas de medición sencillas. Hay muy escasa evidencia en la India
del estudio de problemas geométricos que podríamos llama clásicos,
o de curvas distintas a la circunferencia, e incluso las secciones
cónicas parecen haber sido ignoradas por los hindues, lo mismo que
por los chinos. En cambio a los matemáticos hindues les fascinaban
las cuestiones numéricas, ya tuvieran que ver solamente con las
operaciones aritméticas usuales o con la resolución de ecuaciones
determinadas e indeterminadas. La suma y la multiplicación se hacían
en la India casi de la misma manera como las hacemos hoy, excepto
en que los hindues parecen haber preferido al principio escribir
los números con las unidades de orden menor a la izquierda, y procedían
por lo tanto de izquierda a derecha, utilizando pequeñas pizarras
cubiertas con pintura blanca no permanente que se iba quitando al
escribir sobre ellas, o bien una tabla cubierta de arena o harina.
Ente los métodos utilizados para multiplicar había uno que se conoce
con varios nombres distintos: multiplicación en gelosia o multiplicación
en celdillas o en cuadrilátero. Se recurrirá a dos ejemplos a fin
de ilustrar el método.
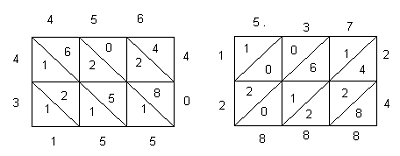
En el primero de
ellos el numero 456 aparece multiplicado por 34; el multiplicando
esta escrito en la parte superior del retículo y el multiplicador
a la izquierda, y los productos parciales ocupan las celdas cuadradas,
de manera que al sumar los dígitos en diagonal de arriba a la izquierda
abajo a la derecha se obtiene el producto 15.504 que aparece en
la parte inferior y derecha el rectángulo. En la otra figura se
indica que los datos pueden ser ubicados también de otras maneras;
aquí se ve el multiplicando 537 situado de nuevo en la parte superior
y el multiplicador 24 en cambio a la derecha, mientras que el producto
12.888 se lee por la izquierda y la parte inferior del rectángulo.
Son posibles aún otras modificaciones de detalle, pero, en su principio
fundamental, la multiplicación por gelosia es la misma que la nuestra,
desde luego, y la distribución de los dígitos por celdillas no es
más que un hábil recurso para evitar el trabajo mental de ‘llevar’
de un lugar al siguiente las decenas que van a pareciendo en los
productos parciales; la única operación de ‘llevar’ que
no se evita en este método es la que resulta al sumar al final los
productos parciales diagonalmente.
La división larga
No se sabe
donde tuvo su origen el método de multiplicación por gelosia, pero
parece lo más probable que fuera en la India, puesto que allí se
utilizaba ya en el siglo XII como mínimo, y de la india parece ser
que se extendió a China y Arabia. De los árabes pasó a Italia durante
los siglos XIV y XV, y aquí fue donde recibió en nombre de gelosia
debido a la semejanza del diagrama con las rejillas de madera que
adornaban y protegían las ventanas en Venecia y otras ciudades italianas.
Los árabes, y a través de ellos más tarde los europeos, adoptaron
la mayor parte de los artificios aritméticos de los hindues, y por
lo tanto es muy probable que también provenga de la India el método
de ‘división larga’ conocido como el método de la galera,
por su semejanza con un barco con las velas desplegadas. Supóngase
la división de 44977 por 382; primero aparece hecha la división
por el método moderno, y luego por el método de la galera. Este
segundo se parece mucho al primero, excepto en que el dividendo
aparece en el medio, ya que las restas se hacen cancelando los dígitos
y poniendo las diferencias encima de los minuendos y no debajo.
Así pues, el resto final aparece en la parte superior derecha y
no en la parte inferior.
117
382)44977
382
677
382
2957
2674
283 |
2
23
398
16753
382 44977 117
38224
387
26 |
El proceso
reproducido es fácil de seguir si tenemos en cuenta que los dígitos
de un substraendo dado, como el 2674, o de una diferencia dada como
la 2957, no figuran todos ellos necesariamente en una misma fila,
y que los substraendos aparecen escritos por debajo de la linea
central y las diferencias por encima; por otra parte la posición
en una columna es importante, pero no la posición en una fila. El
cálculo de raíces probablemente siguió un esquema análogo al de
la galera, ligado con la época posterior en la forma del triángulo
de Pascal, pero los matemáticos hindues no daban nunca las explicaciones
de sus cálculos ni demostraciones de sus reglas; es posible que
las influencias china o babilónica jugaran un papel importante en
el proceso de la evolución del cálculo de raíces. Se dice que ‘la
prueba de los nueve’ es un invento hindú, pero parece que los
griegos ya conocían esta propiedad mucho antes, aunque no la usaron
de una manera general, y que este método se popularizó solamente
con los árabes hacia el siglo XI.
Brahmagupta
Los últimos párrafos
pueden dejar la impresión injustificada de que en la matemática
hindú hubo un alto grado de uniformidad, puesto que varias veces
se ha calificado diversos desarrollos simplemente como ‘de
origen hindú’, sin especificar el período al que corresponden.
El problema esta precisamente en que la cronología hindú es muy
insegura. Por ejemplo, el material que aparece en el importante
manuscrito de Bakshali, que contiene una aritmética anónima, data,
según algunos historiadores, del siglo III o IV, según otros, del
siglo VI; según otro, del siglo VIII o IX o más tarde aún, y hay
incluso opiniones que mantienen que puede son ser siquiera de origen
hindú. Se ha situado la obra de Aryabhata alrededor del año 500,
pero la fecha no es segura, ya que hubo dos matemáticos con ese
nombre y no se puede atribuir con seguridad los resultados al más
viejo. La matemática hindú presenta problemas históricos más difíciles
de resolver que la griega, debido a que los autores hindues raramente
mencionan a sus predecesores, a la vez que muestran una sorprendente
independencia en sus planteamientos matemáticos. Así ocurre, por
ejemplo, que Brahmagupta, que vivió en la India central algo más
de un siglo después que Aryabhata, tiene muy poco que ver con su
antecesor que había vivido en la región oriental de la India. Brahmagupta
menciona dos valores de p, el valor práctico 3 y el valor exacto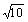 ,
pero no menciona en cambio el valor más aproximado de Aryabhata,
y en la trigonometría que incluye su obra más conocida, el Brahmasphuta
Siddhanta, adopta como radio del circulo el valor 3270 en vez del
3438 de Aryabhata. En un aspecto al menos sí se parece a su antecesor,
y es en la mezcla indiscriminada de resultados correctos e incorrectos.
Brahmagupta calcula el ‘área bruta’ de un triángulo isósceles
multiplicando la mitad de la base por uno de los lados iguales;
para el triangulo escaleno de base 14 y lados 13 y 15 calcula el
‘área bruta’ multiplicando la mitad de la base por la
media aritmética de los otros dos lados. En cambio, para hallar
en ‘área exacta’ utiliza la fórmula de Arquímedes–Herón.
Para el radio de la circunferencia circunscrita a un triángulo da
lo equivalente al resultado trigonométrico correcto ,
pero no menciona en cambio el valor más aproximado de Aryabhata,
y en la trigonometría que incluye su obra más conocida, el Brahmasphuta
Siddhanta, adopta como radio del circulo el valor 3270 en vez del
3438 de Aryabhata. En un aspecto al menos sí se parece a su antecesor,
y es en la mezcla indiscriminada de resultados correctos e incorrectos.
Brahmagupta calcula el ‘área bruta’ de un triángulo isósceles
multiplicando la mitad de la base por uno de los lados iguales;
para el triangulo escaleno de base 14 y lados 13 y 15 calcula el
‘área bruta’ multiplicando la mitad de la base por la
media aritmética de los otros dos lados. En cambio, para hallar
en ‘área exacta’ utiliza la fórmula de Arquímedes–Herón.
Para el radio de la circunferencia circunscrita a un triángulo da
lo equivalente al resultado trigonométrico correcto 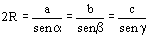 , pero esto no es más que una reformulación
del resultado conocido y por Ptolomeo en su lenguaje de cuerdas.
El resultado quizá más bello de Brahmagupta es su generalización
de la ‘formula de Herón’ para calcular el área de un cuadrilátero;
esta fórmula, , pero esto no es más que una reformulación
del resultado conocido y por Ptolomeo en su lenguaje de cuerdas.
El resultado quizá más bello de Brahmagupta es su generalización
de la ‘formula de Herón’ para calcular el área de un cuadrilátero;
esta fórmula,  donde a, b, c, d son los lados del cuadrilátero y s es el
semiperímetro, aún lleva su nombre, pero la gloria de este descubrimiento
queda un tanto empañada por su fracaso en darse cuenta de que tal
fórmula sólo es correcta en el caso de un cuadrilátero cíclico.
La fórmula correcta para un cuadrilátero arbitrario es donde a, b, c, d son los lados del cuadrilátero y s es el
semiperímetro, aún lleva su nombre, pero la gloria de este descubrimiento
queda un tanto empañada por su fracaso en darse cuenta de que tal
fórmula sólo es correcta en el caso de un cuadrilátero cíclico.
La fórmula correcta para un cuadrilátero arbitrario es  ,donde
a es la semisuma de dos ángulos opuestos en el cuadrilátero. Brahmagupta
da también como regla para hallar el área bruta de un cuadrilátero
la fórmula prehelénica que consiste en multiplicar las medias aritméticas
de los dos pares de lados opuestos. ,donde
a es la semisuma de dos ángulos opuestos en el cuadrilátero. Brahmagupta
da también como regla para hallar el área bruta de un cuadrilátero
la fórmula prehelénica que consiste en multiplicar las medias aritméticas
de los dos pares de lados opuestos.
La fórmula de Brahmagupta
Las contribuciones
de Brahmagupta al álgebra son mucho más importantes que sus reglas
para el cálculo de áreas, ya que se encuentran aquí soluciones generales
de ecuaciones cuadráticas incluyendo las dos raíces aún en casos
en que una de ellas es negativa, de hecho, la primera vez que aparece
sistematizada la aritmética de los números negativos y del cero
es en la obra de Brahmagupta. Reglas esencialmente equivalentes
a las que controlan las operaciones aritméticas con magnitudes negativas
aparecían ya en los teoremas del álgebra geométrica de los griegos,
pero referidas siempre a propiedades de la operación de restar,
tales como, por ejemplo, (a – b)·(c – d)=ac + bd –
ad –bc, pero a los hindues corresponde el mérito de haber dado
un paso decisivo al convertir estas reglasen reglas ‘propiamente
numéricas’ acerca de los números positivos y negativos. Además,
aunque los griegos tuvieron un concepto de la nada y el vacío, no
lo interpretaron nunca como un número, tal como lo hicieron los
hindues. Sin embargo es justamente en este contexto donde Brahmagupta
vuelve a estropear un poco las cosas al afirmar que 0:0=0, mientras
que en la cuestión clave acerca del valor del cuociente a:0, para
a¹ 0, simplemente no se pronuncia:
Positivo dividido
por positivo, o negativo dividido por negativo, es afirmativo (+
: + = - : - = +). Cifra dividido por cifra es nada (0 : 0 = 0).
Positivo dividido por negativo es negativo (+ : - = -). Negativo
dividido por afirmativo es negativo (- : + = -). Positivo o negativo
dividido por cifra es una fracción que la tiene por denominados
(a:0= ) )
Hay que decir también
que los hindues consideraban igualmente como números las raíces
irracionales de otros números, cosa que no hicieron nunca, desde
luego, los griegos. Este paso supuso una ayuda enorme para el álgebra,
y los matemáticos hindues han sido muy elogiados por decidirse a
adoptar esta medida, pero hay que recordar, no obstante, que en
este caso la contribución hindú fue el resultado de una inconsistencia
lógica más que de una profundidad matemática. Ya se ha visto que
los matemáticos hindues carecieron de una distinción clara entre
los resultados exactos y los inexactos, y en consecuencia era lo
más natural que no tomaran en consideración seriamente las diferencias
profundas entre las magnitudes conmensurables y las inconmensurables.
Para ellos no había ningún impedimento en aceptar los números irracionales,
y las generaciones posteriores siguieron su mismo camino de una
manera alegre e ingenua, hasta que en el siglo XIX consiguieron
al fin los matemáticos fundamentar el sistema de los números reales
sobre una base solida.
La matemática hindú consistió, como
se ha dicho, de una mezcla de bueno y malo, pero parte de lo bueno
fue extraordinariamente bueno, y a este respecto Brahmagupta merece
que no se le regateen elogios. El álgebra hindú es notable especialmente
por su desarrollo del análisis indeterminado, al que Brahmagupta
mismo hizo varias contribuciones; para mencionar solo una, aparece
en su obra una regla ara la formación de ternas pitagóricas expresada
en la forma , aunque ésta sea solamente una
forma modificada de la vieja regla babilónica que Brahmagupta pudo
muy bien conocer. La fórmula de Brahmagupta para el área de cuadriláteros,
comentada más arriba, la utilizaba junto con las fórmulas , aunque ésta sea solamente una
forma modificada de la vieja regla babilónica que Brahmagupta pudo
muy bien conocer. La fórmula de Brahmagupta para el área de cuadriláteros,
comentada más arriba, la utilizaba junto con las fórmulas 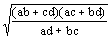 y y  para las diagonales, para hallar cuadriláteros cuyos lados, diagonales
y áreas fueran todos ellos números racionales. Entre estos cuadriláteros
se construye el que tiene por lados a=52, b=25, c=39 y d=60,y por
diagonales 63 y 56. Brahmagupta da como ‘área bruta’ de
este cuadrilátero
para las diagonales, para hallar cuadriláteros cuyos lados, diagonales
y áreas fueran todos ellos números racionales. Entre estos cuadriláteros
se construye el que tiene por lados a=52, b=25, c=39 y d=60,y por
diagonales 63 y 56. Brahmagupta da como ‘área bruta’ de
este cuadrilátero 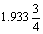 pese al hecho de que en este caso su fórmula da el área
exacta 1.764. pese al hecho de que en este caso su fórmula da el área
exacta 1.764.
La teoría de las ecuaciones indeterminadas
Es evidente
que Brahmagupta amaba la matemática por sí misma, al igual que muchos
de sus paisanos, ya que ningún ingeniero con mentalidad práctica
se hubiera planteado muchas cuestiones tales como las que se planteaba
Brahmagupta cobre los cuadriláteros. Cabe admirar aún más su actitud
matemática al descubrir que él fue el primero que dio con una solución
general de la ecuación lineal diofántica lineal ax + by = c, con
a, b y c enteros. Para que esta ecuación tenga soluciones enteras,
en máximo común divisor entre a y b debe dividir a c, y Brahmagupta
sabía que si a y b eran primos entre sí, entonces todas las soluciones
de la ecuación vienen dadas por las fórmulas x = p + mb, y y = q
– ma, donde m es un entero arbitrario. Brahmagupta estudió
también la ecuación diofántica cuadrática x2 = 1 + py2,
que recibe erróneamente el nombre de John Pell (1611-1685) y que
apareció por primera vez en el problema de los bueyes de Arquímedes.
Esta ecuación de Pell fue resuelta en algunos caso particulares
por el matemático Bhaskara (1114-1185), hindú como Brahmagupta.
Es relamente notable
el mérito de Brahmagupta de dar todas las soluciones enteras de
una ecuación diofántica lineal, mientras que Diofanto se había contentado
con dar una única solución particular de una ecuación indeterminada.
Dado que Brahmagupta utiliza en algunos los mismos ejemplos que
Diofanto, se puede ver de nuevo reforzada la evidencia de una influencia
griega en la India, o bién la posibilidad de que ambos hicieran
uso de una fuente común, verosímilmente de la antigua Babilonia.
Un detalle interesante a subrayar es el que el álgebra de Brahmagupta
es sincopada, como la de Diofanto: la suma se indica por una simple
yuxtaposición, la resta colocando un punto sobre el sustraendo,
y la división escribiendo el divisor debajo del dividendo como en
nuestra notación para las fracciones, pero sin la barra separadora.
Las operaciones de multiplicación y de ‘evolución’ (extracción
de raíces), así como las cantidades incógnitas vienen representadas
por medio de abreviaturas de las palabras correspondientes.
Bhaskara
La India
produjo un cierto número de matemáticos medievales tardíos, pero
sólo se analizará la obra de uno de ellos, Bhaskara, el matemático
más importante del siglo XII y el que completo algunos huecos en
la obra de Brahmagupta, como hizo al dar una solución de la ecuación
de Pell y al enfrentarse al problema de la división por cero. Aritóteles
ya había hecho orservar que no hay ninguna razón en la que un número
tal como cuatro exceda al número cero, pero lo cierto es que la
aritmética del cero no formó parte de la matemática griega, y Brahmagupta
no sa había pronunciado sobre la división de un número distinto
de cero por cero. Así pues, la primera vez que nos encontramos con
la afirmación de que tal cuociente es infinito es en el VijaGanita
de Bhaskara.
Proposición: Dividendo
3. Divisor 0. Cociente la fracción 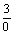 .
Esta fracción de la que el denominador es cifra se llama cantidad
infinita. En esta cantidad que consiste en lo que tenga cifra como
divisor, no hay alteración posible por mucho que se añada o se extraiga,
lo mismo que no hay cambio en Dios infinito e inmutable .
Esta fracción de la que el denominador es cifra se llama cantidad
infinita. En esta cantidad que consiste en lo que tenga cifra como
divisor, no hay alteración posible por mucho que se añada o se extraiga,
lo mismo que no hay cambio en Dios infinito e inmutable
Esta proposición
suena muy prometedora, pero inmediatamente a continuación se revela
una falta de entendimiento claro de la situación por parte de Bhaskara
al afirmar que 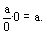
Bhaskara fue el
último matemático medieval importante de la india, y su obra representa
la culminación de las contribuciones hindues anteriores a su época.
En su tratado más conocido, el Lilavati, reunió Bhaskara problemas
diversos procedentes de Brahmagupta y de otros matemáticos, añadiéndoles
nuevas observaciones de su propia cosecha. El título mismo del libro
puede ser tomado como un buen ejemplo de la calidad desigual del
pensamiento hindú, al menos desde un punto de vista occidental,
ya que el nombre al que se reduce el título es precisamente el de
la hija de Bhaskara que, según la leyenda, perdió la oportunidad
de casarse debido a la confianza de su padre en sus predicciones
astrológicas. Bhaskara había calculado que su hija sólo podría casarse
en condiciones favorables a una hora concreta de un determinado
día; el día que había de ser su afortunado casamiento la impaciente
muchacha se encontraba observando atentamente la clepsidra (reloj
de agua), inclinada sobre ella, mientras se iba acercando la hora
de su boda, cuando de pronto cayo al agua inadvertidamente una de
las perlas de su tocado, obstruyendo así la salida del agua de la
clepsidra. Como era de esperar, antes de que se advirtiera el desgraciado
accidente había transcurrido ya la hora propicia, y el padre, para
tratar de consolar a la desdichada muchacha, puso su nombre al libro
comentado.
El Lilavati
El Lilavati,
lo mismo que el VijaGanita, contiene numerosos problemas que tratan
los problemas favoritos de los hindues: ecuaciones lineales y cuadráticas,
tanto determinadas como indeterminadas, siendo problemas de medida
de áreas, progresiones aritméticas y geométricas, raíces, ternas
pitagóricas u otros. El problema del bambú roto popular también
en China e incluido ya por Brahmagupta, aparece aquí en la forma
siguiente. Si un bambú de 32 codos de altura ha sido roto por el
viento de tal manera que su extremo superior queda apoyado en el
suelo a una distancia de 16 codos de su base, ¿a qué altura sobre
el suelo se produjo la fractura? Otro problema en que se utiliza
el teorema de Pitágoras es el siguiente: Un pavo real se encuentra
posado en el extremo de un poste vertical en cuya base hay un agujero
de culebra; observando la culebra a una distancia del pie del poste
igual a tres veces su altura, el pavo real se lanza sobre ella en
linea recta mientras la culebra intenta ganar su agujero. Si el
pavo real captura a la culebra cuando ambos han recorrido la misma
distancia ¿a cuántos codos e distancia del agujero se produjo la
captura?
Estos dos problemas
ilustran muy bien el carácter heterogéneo del Lilavati, puesto que,
a pesar de su aparente semejanza y del hecho de que se pida una
única solución, uno de los problemas es determinado y el otro indeterminado.
Al tratar de círculos y esferas, no consigue tampoco el Lilavati
distinguir entre resultados exactos y sólo aproximados; el área
del círculo, por ejemplo, se expresa correctamente como un cuarto
de la circunferencia por el diámetro, y el volumen de la esfera
como un sexto del producto del área por el diámetro, pero en cambio
Bhaskara sugiere como razón de la circunferencia al diámetro o bien
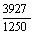 o bien el ‘valor bruto’
de o bien el ‘valor bruto’
de  .
El primero es equivalente a la razón que menciona, pero no utiliza,
Aryabhata, pero nada nos hace sospechar, ni en Bhaskara ni en ningún
otro matemático hindú, que fueran conscientes de que todas las razones
propuestas eran sólo aproximaciones. Sin embargo, Bhaskara se apresura
a condenar severamente a sus predecesores por haber utilizado las
fórmulas de Brahmagupta para el área y las diagonales de un cuadrilátero
en general, basándose en su acertada observación de que un cuadrilátero
no queda inequívocamente determinado por sus lados. Parece evidente,
en cambio, que no se dio cuenta de que las fórmulas en cuestión
si que son correctas en todos los cuadriláteros cíclicos. .
El primero es equivalente a la razón que menciona, pero no utiliza,
Aryabhata, pero nada nos hace sospechar, ni en Bhaskara ni en ningún
otro matemático hindú, que fueran conscientes de que todas las razones
propuestas eran sólo aproximaciones. Sin embargo, Bhaskara se apresura
a condenar severamente a sus predecesores por haber utilizado las
fórmulas de Brahmagupta para el área y las diagonales de un cuadrilátero
en general, basándose en su acertada observación de que un cuadrilátero
no queda inequívocamente determinado por sus lados. Parece evidente,
en cambio, que no se dio cuenta de que las fórmulas en cuestión
si que son correctas en todos los cuadriláteros cíclicos.
Ya se ha dicho que
muchos de los problemas de Bhaskara que aparecen en el Lilavati
y en el VijaGanita provienen de fuentes anteriores, y por lo tanto
no constituye una sorpresa el ver al autor mostrando un gran dominio
de la situación a tratar problemas de análisis indeterminado. Por
lo que se refiere a la ecuación de Pell x2 = 1 + py2,
de la que ya se había ocupado anteriormente Brahmagupta, Bhaskara
da soluciones particulares para los cinco valores del parámetro
p=8, 11, 32, 61 y 67; para la ecuación x2 = 1 + py2,
por ejemplo, da la solución x=1.776.319.049, y = 22.615.390. Esto
constituye sin duda una verdadera hazaña de cálculo, y sólo comprobar
que la solución es correcta pone a prueba la paciencia.
Los libros de Bhaskara
están llenos, por otra parte, de ejemplos variados de problemas
diofánticos.
Ramanujan
Bhaskara
murió a finales del siglo XII, y durante varios siglos a partir
de esa fecha fueron muy pocos los matemáticos de estatura comparable
que aparecieron en la India. Es interesante, sin embargo, hacer
notar aquí precisamente que Srinivasa Ramanujan (1887-1920) tenía
la misma habilidad manipuladora en aritmética y en álgebra que se
ha encontrado en Bhaskara. En la obra de Ramanujan nos encontramos
también con el aspecto desorganizado, la potencia del razonamiento
intuitivo y el desprecio por la geometría que aparecían de manera
relevante en sus predecesores. Aunque es posible que estas características
se desarrollaran quizá en Ramanujan de una manera especial por su
formación autodidacta, no se puede por menos que observar lo sorprendentemente
distinto que fue el desarrollo de la matemática en la India de cómo
lo había sido en Grecia. Incluso cuando los hindues adoptaron conocimientos
tomados de sus vecinos, reestructuraron estos materiales a su peculiar
manera. A pesar de que sus actitudes e intereses estaban más próximas
a las de los chinos que a las de los griegos, no compartieron la
fascinación que sentían estos últimos por los métodos exactos de
aproximación, tales como los que conducen al método de Horner, y
a pesar también de que compartían con los mesopotámicos un punto
de vista preponderantemente algebraico, tendieron a evitar el sistema
de numeración sexagesimal en álgebra. En resumen, los eclécticos
matemáticos hindues adoptaron y desarrollaron solamente aquellos
aspectos que les atraían y, desde un cierto punto de vista al menos,
puede decirse que fue desafortunado el hecho de que su primer amor
haya sido la teoría de números en general y al análisis indeterminado
en particular, porque el crecimiento y desarrollo posterior de la
matemática no iba a surgir de estos campos, la geometría analítica
y el cálculo infinitesimal tuvo raíces griegas y no hindues, y el
álgebra europea moderna provenía más de los países más bien que
de la India. Hay sin embargo, en la matemática moderna al menos
dos cosas lo que debe la matemática a la India en su desarrollo,
lo mismo que a tantos otros países. La trigonometría de la función
seno proviene verosímilmente de la India, y nuestro sistema de numeración
actual para los enteros recibe con toda propiedad el nombre de sistema
Hindú-Árabe para indicar su probable origen en la India y su divulgación
a través de Arabia. |

