| Las civilizaciones
de China y de la India son mucho más antiguas que las de Grecia
y Roma, aunque no más que las que surgieron en los valles de Mesopotamia
y del Nilo; ambas se remontan a la llamada Edad Potámica, mientras
que las culturas griega y romana se desarrollaron durante la Edad
Talásica. Aunque las civilizaciones que tuvieron su cuna en las
cuencas de los ríos Amarillo y Yangtze son comparables en Edad a
las que nacieron a lo largo del Nilo o entre el Eufrates y el Tigris,
los registros cronológicos en el caso de China son mucho menos fiables
que los que existen para Egipto y Babilonia. La operación de fechar
los documentos matemáticos chinos no es nada fácil y, por ejemplo,
las estimaciones que se han hecho acerca del Chou Pei Suan Ching,
considerado generalmente como el más antiguo de los clásicos de
contenido matemático, difieren entre sí en casi mil años; el problema
se complica por el hecho de que esta obra pudiera muy bien ser debida
a varios autores de diferentes épocas. Algunos historiadores consideran
el Chou Pei como un buen ejemplo de lo que era la matemática china
del 1200 a.C. aproximadamente, pero hay otros que sitúan la obra
en el primer siglo anterior a nuestra era. Una fecha en torno al
300 a.C. podría parecer razonable, por lo tanto, poniéndola así
en estrecha competencia con otro tratado, el Chui-chang suan-shu,
escrito hacia el 250 a.C, es decir poco antes del advenimiento de
la dinastía Han (202 a.C.) Las palabras "Chou Pei" parecen
referirse al uso del gnomon para el estudio de las órbitas circulares
en los cielos, y le libro con el mismo titulo trata, de hecho, de
cálculos astronómicos, aunque incluya también una introducción a
las propiedades del triangulo rectángulo, así como algunas cosas
sobre el uso de las fracciones. El libro esta escrito en forma de
dialogo entre un príncipe y su ministro sobre el calendario; el
ministro explica a su soberano que el arte de los números deriva
del circulo y del cuadrado, de los que el cuadrado pertenece a la
tierra y el circulo a los cielos. El Chou Pei nos revela que en
China la geometría, tal como en Egipto, debió surgir de la agrimensura,
y que, como pasaba en Babilonia, la geometría china se reducía a
un ejercicio numérico de aritmética y álgebra. Parece haber en él
algunas indicaciones relativas al teorema de Pitágoras, un teorema
tratado, en todo caso, algebraicamente por los chinos.
Los Nueve Capítulos
Casi tan antiguo
como el Chou Pei es el Chui-chang suan-shu o los "Nueve capítulos
sobre el arte Matemático", quizá la obra que ejerció mayor
influencia de entre todos los libros matemáticos chinos. Este libro
incluye 246 problemas sobre agrimensura, agricultura, compañía,
ingeniería, impuestos, calculo, resolución de ecuaciones y propiedades
de los triángulos rectángulos. Mientras que los griegos de la misma
época escribían tratados expositivos sistemáticos, ordenados de
manera lógica, los chinos se dedicaban a repetir la vieja costumbre
de los babilonios y egipcios de coleccionar conjuntos de problemas
concretos. También aparece en los "nueve capítulos", el
uso del método de "falsa posición", por la invención de
este procedimiento, lo mismo que el origen de la matemática china
en general, parece haber sido independiente de toda influencia occidental.
En las obras matemáticas
chinas sorprende la abigarrada mezcla de resultados exactos e inexactos,
primitivos y sofisticados. Se dan reglas correctas para calcular
el área de triángulos, rectángulos y trapecios; el área del circulo
se calcula tomando los tres cuartos del cuadrado construido sobre
el diámetro, o bien, un doceavo de cuadrado de la circunferencia,
lo cual sería un resultado correcto si tomamos 3 como valor de p
, pero para el área de un segmento de circulo se utiliza el resultado
aproximado de  , donde s es la
sagita (es decir, el radio menos la apotema del segmento) y c es
la cuerda base del segmento. Hay algunos problemas que están resueltos
por medio de reglas de tres, y en otros se encuentran raíces cuadradas
e incluso cubicas. El capitulo ocho tiene importancia por la resolución
de problemas que conducen a sistemas de ecuaciones lineales, utilizando
números positivos y negativos; el ultimo problema de este capitulo,
por ejemplo, plantea la resolución de un sistema de cuatro ecuaciones
con cinco incógnitas y el tema de las ecuaciones indeterminadas
va a quedar como uno de los favoritos de los pueblos orientales.
El capitulo noveno incluye diversos problemas sobre triángulos rectángulos,
algunos de los cuales reaparecerán más tarde en la India y Europa:
uno de ellos pide calcular la profundidad de un estanque circular
de 10 pies cuadrados de superficie, sabiendo que una caña que crece
en su centro y que asoma un pie por encima del agua, alcanza exactamente
la superficie si se la dobla hasta el borde del estanque. Otro de
los problemas es el del bambú roto: Hay un bambú de 10 pies de altura
que se ha roto de manera tal que el extremo superior se apoya en
el suelo a una distancia de 3 pies de la base; se pide calcular
a que altura se ha producido la rotura. , donde s es la
sagita (es decir, el radio menos la apotema del segmento) y c es
la cuerda base del segmento. Hay algunos problemas que están resueltos
por medio de reglas de tres, y en otros se encuentran raíces cuadradas
e incluso cubicas. El capitulo ocho tiene importancia por la resolución
de problemas que conducen a sistemas de ecuaciones lineales, utilizando
números positivos y negativos; el ultimo problema de este capitulo,
por ejemplo, plantea la resolución de un sistema de cuatro ecuaciones
con cinco incógnitas y el tema de las ecuaciones indeterminadas
va a quedar como uno de los favoritos de los pueblos orientales.
El capitulo noveno incluye diversos problemas sobre triángulos rectángulos,
algunos de los cuales reaparecerán más tarde en la India y Europa:
uno de ellos pide calcular la profundidad de un estanque circular
de 10 pies cuadrados de superficie, sabiendo que una caña que crece
en su centro y que asoma un pie por encima del agua, alcanza exactamente
la superficie si se la dobla hasta el borde del estanque. Otro de
los problemas es el del bambú roto: Hay un bambú de 10 pies de altura
que se ha roto de manera tal que el extremo superior se apoya en
el suelo a una distancia de 3 pies de la base; se pide calcular
a que altura se ha producido la rotura.
Los Cuadrados mágicos
Los chinos han sido
siempre muy aficionados a los diseños armónicos, aritméticos o geométricos,
y no es sorprendente por lo tanto que el primer ejemplo registrado
de cuadrado mágico haya aparecido aquí. El cuadrado
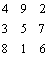
le fue comunicado a los hombres por
una tortuga del río Lo, según la leyenda, en los días del emperador
Yii, famoso ingeniero hidráulico. El interés por este tipo de modelos
es sin duda lo que llevo al autor de los nueve capítulos a resolver
el sistema de ecuaciones lineales

mediante operaciones sobre las columnas
de la matriz

para reducirla a la forma

donde esta segunda forma representa
el sistema de ecuaciones
36z = 99 , 5y + z = 24 , 3x + 2y + z
= 39
del cual se pueden obtener fácilmente,
y de una manera sucesiva, los valores de z, y, x.
Los numerales a base de varillas
Si la matemática
china hubiera disfrutado de una continuidad sin interrupciones basada
en la tradición, es posible que algunas de las sorprendentes anticipaciones
de ciertos métodos modernos pudieran haber llegado a modificar de
una manera significativa el desarrollo de la matemática, pero la
cultura china vio a veces seriamente dificultado su desarrollo por
bruscas rupturas. El año 213 a.C. por ejemplo, ordenó el emperador
chino la quema de libros, excluidos probablemente los de tipo técnico.
Algunas obras debieron obviamente sobrevivir, o bien porque se conservasen
copias en forma clandestina o por simple transmisión oral de obras
aprendidas integramente de memoria. De esta forma el saber consiguió
persistir superando las dificultades, con el énfasis puesto, en
el caso de la matemática, en los problemas relativos al calendario
y el comercio.
Parece haber existido
algún tipo de contacto entre la India y China, así como entre China
y el Oeste, pero los historiadores difieren al evaluar la extensión
y la dirección de las influencias ejercidas. La tentación natural
de ver una influencia babilónica o griega en China, por ejemplo,
choca con el problema importante de que los chinos nunca hicieron
uso de las fracciones sexagesimales. El sistema de numeración chino
permaneció esencialmente decimal, con notaciones sorprendentemente
diferentes de las utilizadas en otros países. En china se utilizaron
dos esquemas de notación distintos desde los tiempos más primitivos.
En uno de ellos predominaba el principio multiplicativo, mientras
que en el otro se utilizaba una forma de notación posicional. En
el primero había cifras distintas para los dígitos del uno al diez,
y otras cifras para las potencias de diez, y en la forma escrita
los dígitos que ocupaban una posición impar (de izquierda a derecha
o de abajo arriba) se multiplicaban por sus sucesores; así por ejemplo
el numero 678 se escribiría como un 6 seguido por el símbolo para
el 100, después un siete seguido del símbolo para 10, y por ultimo
el símbolo para el 8.

En el sistema de
los "numerales a base de varillas", los dígitos del 1
al 9 se representaban por

y los nueve primeros múltiplos de 10
por utilizando estos 18 símbolos alternadamente en las posiciones
de derecha a izquierda, se pueden expresar números tan grandes como
se desee; por ejemplo, el numero 56.789 se representaría por

Al igual que en Babilonia,
solo de una manera tardía apareció un símbolo para representar una
posición vacía. En una obra del año 1247 se escribe el numero 1.405.536
usando un símbolo redondo para el cero, de la forma

En ocasiones, como
pasa con algunas formas del triangulo aritmético que datan del siglo
XIV, las varillas o palotes verticales y horizontales aparecen intercambiadas.
La época exacta en
la que aparecieron los numerales a base de varillas no se ha podido
determinar, pero es seguro que ya se usaban varios siglos antes
de nuestra era, es decir, mucho antes de que se adoptara el sistema
de notación posicional en la India.
El uso de un sistema
posicional centesimal más que decimal en China resultó conveniente
para la adaptación de los cálculos a la tabla de calcular; las distintas
notaciones para las potencias de 10 permitirán a los chinos utilizar
unas tablas de calcular con columnas verticales sin marca, y hasta
el siglo VIII el lugar que debía ocupar un cero se dejaba simplemente
en blanco. Aunque en los textos anteriores al año 300 de nuestra
era los números y las tablas de multiplicar se escribían en palabras,
de hecho, los cálculos se realizaban con numerales a base de varillas
sobre una tabla de calcular.
El ábaco y las fracciones decimales
Los numerales a base
de varillas del año 300 a.C. aproximadamente no eran una simple
notación para escribir los resultados de una computación, sino que
los administradores, por ejemplo, llevaban consigo una bolsa que
contenía una colección de varillas concretas de bambú, marfil o
hierro, que utilizaban como instrumentos para hacer sus cálculos.
Las varillas para contar las manejaban los chinos con tanta habilidad
que un escritor del siglo XI nos las describe como "volando
con tal rapidez de un lado a otro que el ojo no podría seguir su
movimiento". Los pasos consistentes en cancelaciones de cantidades
iguales se podían llevar a cabo probablemente con mayor rapidez
usando las varillas en una tabla de calcular que en los cálculos
escritos y, de hecho, resulto tan eficaz el uso de las varillas
y de las tablas de calcular, que el ábaco o marco de calcular rígido,
con bolas movibles a lo largo de barras paralelas no se comenzó
a utilizar tan tempranamente como se había supuesto de manera general.
Las primeras descripciones claras que nos encontramos de sus formas
modernas, conocidas en China con en nombre de Sua Phan y en Japón
como Soroban, datan del siglo XVI, aunque ciertas anticipaciones
podrían haber sido utilizadas quizá hasta mil años antes. La palabra
latina abacus probablemente se deriva de la palabra semítica abq
que significa polvo, lo cual nos indicaría que en otros países,
lo mismo que en China, este aparato evolucionó a partir de una bandeja
llana de polvo o arena y que se utilizaba como tabla de calcular.
Es posible, aunque no seguro en absoluto, que el uso de la tabla
de calcular sea anterior en China que en Europa, pero en cualquier
caso no se dispone de fechas precisas y fiables. Exactamente cuándo
dieron paso estos utensilios al ábaco propiamente dicho es una cuestión
difícil de decidir, así como tampoco se puede decir si la aparición
del ábaco en China, en Arabia y en Europa se debió o no a inventos
independientes entre sí. El ábaco árabe tenía 10 bolas en cada alambre
y no tenía barra central, mientras que el chino tenía en cada alambre
5 bolas por debajo de la barra central y dos por encima, cada una
de las bolas superiores en un mismo alambre del ábaco chino equivale
a cinco de las inferiores, y para registrar un numero se hacen deslizar
el numero correspondiente de bolas hacia la barra central que las
separa unas de otras.
Modelo de ábaco chino
 No se puede considerar completa la descripción
del sistema de numeración chino sin hacer referencia al uso de las
fracciones. Los chinos conocían bien las operaciones con fracciones
ordinarias, hasta el punto de que en este contexto hallaban el mínimo
común denominador de varias fracciones. Al igual que hacían en otras
materias, también aquí establecían analogías con los distintos sexos,
refiriéndose al numerador como "el hijo" y al denominador
como "la madre"; el énfasis generalizado en toda la cultura
china sobre los principios del yin y el yang hacia más fácil seguir
las reglas para manipular fracciones. Más importante que estas curiosidades
era, no obstante, la tendencia a la decimalización de las fracciones
en China. La adopción de un sistema decimal en pesos y medidas dio
como resultado que se impusiera el hábito decimal en el manejo de
las fracciones, que puede rastrearse, según se dice, tan lejos en
el tiempo como el siglo XIV a.C. Algunas veces se adoptaron ciertas
artimañas de carácter decimal para aligerar un poco la manipulación
de las fracciones; así, por ejemplo, en un comentario a los nueve
capítulos que data del primer siglo de nuestra era, nos encontramos
con el uso de unas reglas que hoy nos son muy conocidas para el
calculo de raíces cuadradas y cubicas, equivalentes a escribir No se puede considerar completa la descripción
del sistema de numeración chino sin hacer referencia al uso de las
fracciones. Los chinos conocían bien las operaciones con fracciones
ordinarias, hasta el punto de que en este contexto hallaban el mínimo
común denominador de varias fracciones. Al igual que hacían en otras
materias, también aquí establecían analogías con los distintos sexos,
refiriéndose al numerador como "el hijo" y al denominador
como "la madre"; el énfasis generalizado en toda la cultura
china sobre los principios del yin y el yang hacia más fácil seguir
las reglas para manipular fracciones. Más importante que estas curiosidades
era, no obstante, la tendencia a la decimalización de las fracciones
en China. La adopción de un sistema decimal en pesos y medidas dio
como resultado que se impusiera el hábito decimal en el manejo de
las fracciones, que puede rastrearse, según se dice, tan lejos en
el tiempo como el siglo XIV a.C. Algunas veces se adoptaron ciertas
artimañas de carácter decimal para aligerar un poco la manipulación
de las fracciones; así, por ejemplo, en un comentario a los nueve
capítulos que data del primer siglo de nuestra era, nos encontramos
con el uso de unas reglas que hoy nos son muy conocidas para el
calculo de raíces cuadradas y cubicas, equivalentes a escribir 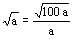 y y  , y que facilitan la decimalización al hacer extracciones
de raíces. , y que facilitan la decimalización al hacer extracciones
de raíces.
La idea de los números negativos parece
no haber ocasionado muchas dificultades a los chinos, puesto que
estaban acostumbrados a calcular utilizando dos conjuntos de varillas,
uno de color rojo para representar los números o coeficientes positivos
y el otro de color negro para los negativos. Sin embargo, no aceptaron
la idea de que un numero negativo pudiera ser una solución de una
ecuación.
Los valores de p en China
La matemática china
primitiva es tan distinta de la que se hacia en la misma época en
otros lugares del mundo que parecería completamente justificada
la hipótesis de un desarrollo independiente por completo. En cualquier
caso, lo que parece que puede afirmarse con toda seguridad es que
si hubo alguna intercomunicación antes de 400, entonces salió más
matemática de China que entro, pero en cambio para periodos posteriores
la cuestión se hace más difícil de responder. El uso del valor 3
para p en la matemática china primitiva
puede servir como argumento a favor de una hipotética dependencia
de Mesopotamia, especialmente a la vista de que la búsqueda de valores
cada vez más exactos fue más persistente en China que en ningún
otro sitio, desde los primeros siglos de la era cristiana. En este
proceso nos encontramos con los valores  ,
y en el siglo III aparece Liu Hui, importante comentarista de los
nueve capítulos, que obtiene en valor 3,14 usando un polígono regular
de 96 lados y la aproximación mucho mejor 3,14159 considerando un
polígono de 3072 lados. En la refundición que hizo Liu Hui de los
Nueve capítulos hay muchos problemas sobre el calculo de medidas
, incluyendo la determinación correcta del volumen de un tronco
de pirámide de base cuadrada, para el tronco de cono circular se
aplica una formula análoga, pero con el valor 3 para p
. Una regla sorprendente en la que da el volumen del tetraedro con
dos aristas opuestas perpendiculares como 1/6 del producto de estas
dos aristas por el segmento perpendicular común. Para resolver ecuaciones
lineales se utiliza el método de la falsa posición, pero hay también
otros resultados algebraicos más sofisticados tales como la resolución
por medio de un esquema matricial de un problema diofántico en el
que aparece un sistema de cuatro ecuaciones con cinco incógnitas.
La resolución aproximada de ecuaciones de grados más altos parece
haber sido efectuada recurriendo a un artificio análogo al que nosotros
conocemos como método de Horner. Liu Hui incluye también en su obra
sobre los nueve capítulos gran cantidad de problemas sobre calculo
de alturas de torres inaccesibles y de árboles en laderas de montañas. ,
y en el siglo III aparece Liu Hui, importante comentarista de los
nueve capítulos, que obtiene en valor 3,14 usando un polígono regular
de 96 lados y la aproximación mucho mejor 3,14159 considerando un
polígono de 3072 lados. En la refundición que hizo Liu Hui de los
Nueve capítulos hay muchos problemas sobre el calculo de medidas
, incluyendo la determinación correcta del volumen de un tronco
de pirámide de base cuadrada, para el tronco de cono circular se
aplica una formula análoga, pero con el valor 3 para p
. Una regla sorprendente en la que da el volumen del tetraedro con
dos aristas opuestas perpendiculares como 1/6 del producto de estas
dos aristas por el segmento perpendicular común. Para resolver ecuaciones
lineales se utiliza el método de la falsa posición, pero hay también
otros resultados algebraicos más sofisticados tales como la resolución
por medio de un esquema matricial de un problema diofántico en el
que aparece un sistema de cuatro ecuaciones con cinco incógnitas.
La resolución aproximada de ecuaciones de grados más altos parece
haber sido efectuada recurriendo a un artificio análogo al que nosotros
conocemos como método de Horner. Liu Hui incluye también en su obra
sobre los nueve capítulos gran cantidad de problemas sobre calculo
de alturas de torres inaccesibles y de árboles en laderas de montañas.
La fascinación que
ejerció sobre los chinos el número p alcanzo
su punto más alto en la obra de Tsu Chu’ng-Chih (430-501).
Uno de sus valores era el conocido valor arquimediano  , al que califica de "inexacto";
su valor "exacto" era , al que califica de "inexacto";
su valor "exacto" era  . Si uno se encuentra obsesionado buscando posibles influencias
occidentales, puede explicar esta aproximación tan buena que no
se vio igualada en ninguna parte hasta el siglo XV restando los
numeradores y denominadores respectivamente del valor dado por Arquímedes
al valor dado por Ptolomeo . Si uno se encuentra obsesionado buscando posibles influencias
occidentales, puede explicar esta aproximación tan buena que no
se vio igualada en ninguna parte hasta el siglo XV restando los
numeradores y denominadores respectivamente del valor dado por Arquímedes
al valor dado por Ptolomeo  . Sin embargo, Tsu Chu’ng-Chih
llego incluso más lejos en sus cálculos, ya que dio también 3,1415927
como un "valor por exceso" y 3,1415925 como un "valor
por defecto" para p. Los cálculos
por medio de los cuales llego a estos resultados, ayudado al parecer
por su hijo Tsu Cheng-Chih, estaban contenidos probablemente en
alguno de sus libros que se ha perdido. En cualquier caso sus resultados
fueron muy notables para esta época, y resulta muy oportuno el haber
puesto su nombre a un accidente geográfico de la superficie lunar. . Sin embargo, Tsu Chu’ng-Chih
llego incluso más lejos en sus cálculos, ya que dio también 3,1415927
como un "valor por exceso" y 3,1415925 como un "valor
por defecto" para p. Los cálculos
por medio de los cuales llego a estos resultados, ayudado al parecer
por su hijo Tsu Cheng-Chih, estaban contenidos probablemente en
alguno de sus libros que se ha perdido. En cualquier caso sus resultados
fueron muy notables para esta época, y resulta muy oportuno el haber
puesto su nombre a un accidente geográfico de la superficie lunar.
No debemos
olvidar, sin embargo, que el grado de exactitud alcanzado en el
calculo del valor de p es más una cuestión
de resistencia calculistica que de inteligencia teórica. De hecho,
basta con el teorema de Pitágoras para conseguir una aproximación
tan buena como se desee. Si partimos del perímetro conocido de un
polígono regular de n lados inscrito en una circunferencia, entonces
en perímetro del polígono regular inscrito de 2n lados se puede
calcular por medio de dos aplicaciones del teorema de Pitágoras.
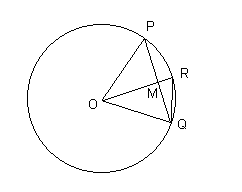
Sea, en efecto, C una circunferencia de centro O y radio r y sea
PQ = s un lado del polígono regular inscrito de n lados, cuyo perímetro
conocemos: Entonces la apotema OM = u viene dada por 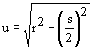 , y por lo tanto también conocemos la sagita MR = v = r
– u , de donde el lado RQ = w del polígono regular inscrito
de 2n lados se puede calcular a partir de la formula , y por lo tanto también conocemos la sagita MR = v = r
– u , de donde el lado RQ = w del polígono regular inscrito
de 2n lados se puede calcular a partir de la formula  ,
y conocemos por ultimo el perímetro 2nw. Este calculo puede abreviarse,
como observo Liu Hui, teniendo en cuenta que w2 = 22rv.
Repitiendo este procedimiento iremos obteniendo aproximaciones cada
vez mejores del perímetro de la circunferencia, en términos del
cual se define p. ,
y conocemos por ultimo el perímetro 2nw. Este calculo puede abreviarse,
como observo Liu Hui, teniendo en cuenta que w2 = 22rv.
Repitiendo este procedimiento iremos obteniendo aproximaciones cada
vez mejores del perímetro de la circunferencia, en términos del
cual se define p.
El álgebra y el método de Horner
Los problemas encontrados
en la matemática china parecen ser a menudo más pintorescos que
prácticos, y, sin embargo, la civilización china produjo un número
de innovaciones técnicas sorprendentemente alto. La utilización
de la imprenta y la pólvora (siglo VIII), así como del papel y de
la brújula marina (siglo XI) fue anterior en China que en cualquier
otro lugar, y anterior también a la época más brillante de la matemática
china, que tuvo lugar durante en siglo XIII, coincidiendo con la
ultima parte del período Sung. En esta época había matemáticos trabajando
en diversos lugares de China, pero las relaciones entre ellos parecen
haber sido escasas y remotas y han llegado a nosotros relativamente
pocos de los tratados que circularon en esos días. El ultimo y a
la vez más importante de los matemáticos fue Chu Shih-Chieh que
floreció hacia los años 1280-1303 a pesar de lo cual se sabe tan
poco sobre el que no se conoce la fecha exacta de su nacimiento
ni muerte. Vivió en Yen-shan, cerca de Peking. Escribió dos tratados,
el primero de ellos, escrito hacia 1299, fue el Suan-hsüeh ch’i-meng
o "Introducción a los estudios Matemáticos" un libro relativamente
elemental que ejerció, sin embargo, gran influencia en Corea y Japón,
aunque en China desapareció más tarde y estuvo perdido hasta su
reaparición en el siglo XIX. Mayor interés histórico y matemático
tiene el Ssu-yüan yü-Chien o "Espejo precioso de los cuatro
elementos", escrito en 1303. Los cuatro elementos a que se
refiere el titulo, que son el cielo, la tierra, el hombre y la materia
representan las cuatro incógnitas de una ecuación. Este libro marca
la cota más alta que alcanzo el desarrollo del álgebra china, y
en él se estudian tanto sistemas de ecuaciones simultaneas como
ecuaciones individuales de grados tan altos como 14. Chu Shih-Chieh
explica en este libro un método de transformaciones que él llama
el fan fa, y cuyo fundamento debe haber aparecido en China mucho
tiempo antes, método que suele conocerse en Occidente como ‘método
de Horner’, matemático que vivió medio milenio más tarde. Para
resolver la ecuación x2 + 252x – 5292 = 0, por ejemplo,
Chu Shih-Chieh obtiene en primer lugar por tanteo la aproximación
19, lo cual significa que la ecuación tiene una raíz entre x=19
y x=20, y a continuación utiliza en fan fa, en este caso la transformación
y = x - 19, para obtener la ecuación y2 + 290y –
143 = 0 con una raíz entre 0 y 1. El valor aproximado de la raíz
buscada es  , y por lo tanto
el correspondiente valor de x es , y por lo tanto
el correspondiente valor de x es  . Para la ecuación x3 – 574 = 0 usa la transformación
y =x – 8, que conduce a y3 + 24y2 + 192y
– 62 = 0 y la raíz buscada viene expresada como . Para la ecuación x3 – 574 = 0 usa la transformación
y =x – 8, que conduce a y3 + 24y2 + 192y
– 62 = 0 y la raíz buscada viene expresada como  ó ó 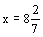 .
En algunos casos Chu Shih-Chieh obtiene aproximaciones decimales
de las raíces. .
En algunos casos Chu Shih-Chieh obtiene aproximaciones decimales
de las raíces.
Los matemáticos del siglo XIII
El llamado método
de Horner era bien conocido en China, como lo demuestra el hecho
de que por lo menos tres matemáticos del período Sung tardío hicieran
uso de procedimientos análogos. Uno de ellos fue Li Chih (1192-1279),
quien vivió en Peking y a quien Khubali Khan ofreció en 1260 un
puesto en el gobierno, el cual Li Chih rehusó con una cortés excusa.
Su libro Ts’e-yuan hai-ching o "Espejo marino de las medidas
del circulo", contiene 170 problemas relativos círculos inscritos
y circunscritos a un triangulo rectángulo y a las relaciones entre
los lados y los radios, donde algunos de estos problemas conducen
a ecuaciones de cuarto grado. Aunque Li Chih no explica su método
de resolución de ecuaciones, entre las cuales hay algunas de grado
6, todo hace pensar que no era muy diferente del utilizado por Chu
Shih-Chieh y más tarde por Horner. Otros dos matemáticos que usaron
el método de Horner fueros Ch’in Chiu-Shao y Yang Hui. El primero
de ellos fue además un ministro y gobernador sin escrúpulos que
tuvo el mérito notable de adquirir enormes riquezas en los cien
días de su mandato. Su Obra Shu Chiu-Chang o "Tratado Matemático
en nueve secciones" marca el punto culminante del análisis
indeterminado chino, con la invención de reglas rutinarias para
resolver problemas de congruencias simultaneas. También aparece
en esta obra el calculo de la raíz cuadrada de 71824 por etapas,
paralelamente a lo que se hace en el método de Horner: partiendo
de 200 como primera aproximación de la raíz de x2 –
71824 = 0, reduce esta raíz en 200 mediante el cambio de incógnita
que conduce a y2 + 400y – 31824 = 0. Para esta segunda
ecuación Ch’in Chiu-Shao encuentra que 60 es una buena aproximación
de la raíz y disminuyéndola en 60 se llega a una tercera ecuación
z2 + 520z – 424 = 0, de la que 8 es raíz, y por
lo tanto tenemos que x = 268. De una manera similar resuelve ecuaciones
cúbicas y cuárticas. El mismo procedimiento de Horner fue utilizado
por Yang Hui, de cuya vida se sabe casi nada y cuya obra sólo se
conserva en parte; entre sus contribuciones que han llegado hasta
nosotros hay que contar los primeros cuadrados mágicos chinos de
orden mayor que tres, incluyendo dos de cada uno de los ordenes
cuatro a ocho y uno de cada uno de los ordenes 9 y 10.
El triangulo Aritmético
Las obras de Yang
Hui incluían también otros resultados acerca de la suma de series
finitas y del llamado "triangulo de Pascal", pero estos
temas son más conocidos por haber aparecidos publicados en el espejo
precioso de Chu Shih-Chieh, con el que se cierra la edad de oro
de la matemática china. Como ejemplos de las muchas sumas de series
finitas que aparecen en el espejo precioso, se puede considerar
las siguientes:

de las cuales no se da, sin embargo,
demostración alguna, ni tampoco parece que el tema haya sido tratado
de nuevo en China hasta casi el siglo XIX. Chu Shih-Chiehs se maneja
con estas sumas por medio del método de diferencias finitas, algunos
elementos del cual parecen remontarse en China al siglo VII, pero
poco después de publicada esta obra el método en cuestión desapareció
por varios siglos.
El espejo precioso
comienza con un diagrama del triangulo aritmético, conocido en Occidente
como Triangulo de Pascal y en este diagrama figuran los coeficientes
de los distintos desarrollos binómicos hasta la octava potencia,
escritos con toda claridad en al sistema de numerales a base de
varillas y con un símbolo redondo para el cero. Chu no pretende
ser el autor de este triangulo, sino que se refiere a él como el
diagrama del viejo método para hallar potencias octavas e inferiores’.
De hecho, ya había aparecido en la obra de Yang Hui una distribución
análoga de los coeficientes hasta la sexta potencia de un binomio,
aunque sin utilizar un símbolo redondo para el cero, y en algunas
obras chinas de hacia el 1100 se encuentran referencias sistemas
de tabulación para el triangulo aritmético, y es probable que dicho
triangulo aritmético tuviera su origen en China más o menos por
estas fechas. Es interesante hacer notar que el descubrimiento por
parte de los chinos del teorema binomial para potencias enteras
positivas, estuvo asociado en su origen a la extracción de raíces
más que al cálculo de potencias. Una forma equivalente de este teorema
la conocía al parecer también Omar Khayyam por la misma época en
que estaba siendo utilizado en China, pero la obra árabe más primitiva
que ha llagado hasta nosotros y que lo incluye se debe a Al-Kashi
y data del siglo XV; por esta época la matemática china ya no podía
equipararse en su desarrollo con la europea ni con la del próximo
oriente, y es muy probable que para ese entonces China importase
más matemática que exportase. Aún queda por resolver, sin embargo,
el espinoso problema de determinar las influencias relativas entre
China y la India durante el primer milenio de nuestra era. |
