Como vimos en la primera parte de estos
artículos, los cifrados monográficos, en los que
se sustituye un carácter por otro de una forma preestablecida
son vulnerables al análisis de frecuencia de aparición
de las letras. Para evitarlo se han desarrollado esquemas basados
en cifrar bloques de letras de una cierta longitud fija. Los esquemas
que desarrollaremos aquí se deben a Hill (hacia 1930).
Para que sea más fácilmente
comprensible lo que vendrá después comenzaremos
por un cifrado digráfico (bloques de 2 caracteres).
Empecemos por cifrar lo siguiente:
E S T
A C I O N
C E N T R
A L X
04 18 19 00 02 08 14 13 02 04 13 19 17 00 11 23
Ahora aplicamos la siguiente
transformación:
C1 = 5*P1 + 17*P2 (mod 26)
C2 = 4*P1 + 15*P2 (mod 26)
Donde P1 y P2 son dos caracteres del
mensaje sin cifrar y C1 C2 los correspondientes cifrados. En nuestro
ejemplo:
C1= 5*4 + 17*18 = 326 = 14 (mod 26)
C2= 4*4 + 15*18 = 286 = 0 (mod 26)
por lo que los dos primeros caracteres del texto
cifrado son O (14) y A (0), aplicando esto a todos los pares de
letras del texto (observa que como el número de letras
es impar debemos añadir una letra, por ejemplo una X al
final del mensaje) se obtiene la siguiente secuencia numérica:
14 0 17 24 16 24 5 17 0 16 24 25 7 16 4 25
es decir: OARYQYFRAQYZHQEZ
(se han suprimido los espacios en blanco del mensaje original
antes de cifrarlo)
Expresado en notación matricial
sería:
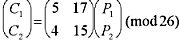
o abreviadamente C=A.P por lo que para descifrar tenemos que
realizar el proceso inverso, es decir P=A'.C donde A' es la matriz
inversa de A módulo 26, y en este caso
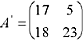
así que la transformación inversa, utilizada para
descifrar sería:
P1 = 17*C1 + 5*C2 (mod 26)
P2 = 18*C1 + 23*C2 (mod 26)
En general si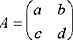 
es la matriz
usada para cifrar, y d=determinante(A)=a*d-b*c se tiene que la
matriz inversa A' será igual a:
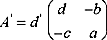
siendo d' el inverso de d módulo 26, en nuestro caso d=5*15-17*4=7
y como mcd(7,26)=1 podemos estar seguros de que d tiene inverso,
en concreto d'=15 ya que 7*15=105=1 (mod 26) al ser 105 múltiplo
de 26 más 1.
En el próximo número acabaremos
de hablar sobre cifrados poligráficos (por bloques) de
Hill, exponiendo la generalización de esto a bloques de
tamaño n y los posibles puntos flacos de este tipo de cifrado.
Me gustaría leer toda clase de
problemas, dudas y sugerencias que tengáis sobre el tema.
Usad el formulario de la página principal.
|
