Se utilizan
también otros métodos que fallan por ser observables,
predecibles o influenciables por nuestro adversario.
Cálculo de la entropía
El segundo paso sería calcular
cuantos bits imposibles de adivinar hemos obtenido. Dicho número
se llama entropía y puede calcularse así:
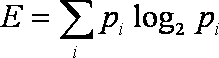
donde i varía desde 1 hasta el número de posibles
valores secretos (que para nosotros serán un conjuntos
contiguo de bits de cierto tamaño, byte, word...) y pi
es la probabilidad de que se de el valor i-esimo.
Si hay 2n diferentes valores
con igual probabilidad, entonces tenemos n bits de información
y un adversario tendría que intentar en promedio 2n-1
valores antes de acertar el valor secreto. En particular, si hay
valores que el adversario sabe que no pueden ocurrir, o que lo
hacen con menor probabilidad, los descartará, centrando
su búsqueda en el resto.
Imaginemos que estamos utilizando un
sistema criptográfico con claves de 128 bits. Imaginemos
además que las claves se obtienen utilizando un generador
de números aleatorios con una semilla de 8 bits. Entonces
y aunque aparentemente hay 2128 claves posibles un
adversario sólo debe probar 28=256 veces (128
en promedio realmente). Solo hay 8 bits de información
en esos 128 de clave.
Realmente estamos interesados en calcular
los bits de entropía por cada bit obtenido. Para ello tendríamos
que dividir la entropía entre el tamaño en bits
de los valores buscados. Es decir si por ejemplo estamos obteniendo
bytes calcularemos J=E/8.
Un paso adicional sería calcular
la entropía absoluta (que abusando de la notación
llamaremos también E) definida como el mínimo de
todos los J posibles cuando el tamaño de los valores varía
entre 1 e infinito. Esta definición depende de disponer
de una cantidad infinita de sucesiones de longitud infinita y
es por tanto principalmente de interés teórico.
Con esta definición dado que todos los generadores de números
pseudoaleatorios son “máquinas con un número
finito de estados” y por tanto periódicas, las secuencias
obtenidas por estos generadores son de entropía 0 y por
tanto inútiles para nuestros propósitos. La razón
es que cuando el tamaño del símbolo es igual al
periodo de nuestro generador la secuencia esta formada por símbolos
iguales repetidos una y otra vez, siendo por tanto 0 la cantidad
de bits utilizables. Una vez más esto es sólo teórico
ya que el periodo de un PRNG (pseudo random number generator)
puede ser mucho más grande que lo que cualquier ordenador
en el universo pueda calcular, sin embargo arroja alguna luz sobre
las limitaciones y naturaleza de los PRNG.
Así pues nos vemos obligado a
calcular una aproximación de la entropía absoluta
a partir de algunas cadenas de valores. Algunas personas usan
el mejor algoritmo de compresión disponible confiando en
que el porcentaje de compresión aproxime E ya que si hubiera
un algoritmo de compresión perfecto, su salida tendría
E=1 por definición.
Si fuera posible calcular una aproximación
de la entropía absoluta a partir de nuestra cadena, el
valor sería el mismo no importa que representación
se tome de la cadena de muestra. Hay transformaciones que preservan
toda la información de la cadena, por ejemplo una transformada
de Fourier, la transformación de Hadamard o el operador
diferencia yi=xi-xi-1 y el número
de bits absolutamente imposibles de adivinar debe permanecer constante
bajo tales transformaciones. Uno puede por tanto evaluar la calidad
de una estimación de la entropía probando su algoritmo
con varias transformaciones de la misma cadena y comparando los
resultados.
De cualquier forma en que uno calcule
su aproximación a la entropía absoluta, uno deber
reducirla aún más para reflejar la fracción
de entropía que un adversario puede haber adquirido adivinando,
interviniendo una habitación o comunicación o creando
alguna desviación en el proceso de generación. Por
ejemplo si uno utiliza la fecha y la hora del sistema que en principio
son unos cuantos bits utilizables, uno debería esperar
que su adversario conozca la fecha, probablemente la hora y quizás
los minutos escogidos de modo que solo nos quedarían unos
bits inferiores aprovechables. Si uno escoge una firma dibujada
con el ratón como fuente de entropía la parte del
trazo que sigue la firma real del autor debe suponerse conocida
y sólo por tanto las pequeñas desviaciones respecto
a aquella cuentan como bits aprovechables.
Una vez calculada de forma satisfactoria
E, debemos tomar esta cantidad como la fracción de los
bits que podemos usar de nuestra secuencia. Específicamente
si estamos usando una función hash (como veremos después)
que produce una salida de K bits entonces debemos pasar a dicha
función K/E bits de nuestra secuencia. Supongamos que estamos
utilizando por ejemplo MD5 que tiene 128 bits de salida, y supongamos
además que hemos calculado E=0.33 (es decir que un tercio
de nuestros bits son aprovechables) entonces deberíamos
pasar a MD5 un bloque de unos 128/0.33 = 388 bits.
Mejorando la “calidad” de los bits obtenidos
Existen algunos requisitos en la distribución
de los números aleatorios. No necesitamos que sigan exactamente
una distribución uniforme pero sí acotar la no-uniformidad
de la distribución. Describamos algunas técnicas
para eliminar sesgos en nuestra secuencia de bits.
1.- Paridad de los datos : consideremos
tomar una larga ristra de bits y aplicarla sobre un 0 o un 1.
La aplicación no conducirá a una distribución
uniforme pero puede estar tan cercana a ella como deseemos. Una
aplicación posible es la paridad de la cadena. Sirve cualquiera
que sea el sesgo de la cadena y es trivial de implementar.
Un pequeño análisis no
mostraría que la cantidad de bits que necesitamos emplear
es N>log(2d)/log(2e) donde d es la diferencia que queremos
que haya entre una distribución uniforme ideal y la nuestra
y e es la probabilidad de que un bit de la cadena sea uno menos
0.5.
Para que la distribución esté
a menos de 0.001 de una distribución 50/50 la siguiente
tabla nos da la longitud de la ristra de bits que debemos utilizar.
Prob(1) |
e |
N |
| 0.50 |
0.00 |
1 |
| 0.60 |
0.10 |
4 |
| 0.70 |
0.20 |
7 |
| 0.80 |
0.30 |
13 |
| 0.90 |
0.40 |
28 |
| 0.95 |
0.45 |
59 |
| 0.99 |
0.49 |
308 |
Por ejemplo la última fila de
la anterior tabla nos muestra que incluso aunque haya un 99% de
unos en nuestra secuencia de bits, la paridad de una cadena de
308 bits estará a menos de 0.001 de una distribución
perfecta 50/50.
2.- Uso de la FFT (transformada rápida
de Fourier): aunque los datos provenientes del “mundo real”
estén fuertemente sesgados y correlados pueden contener
cantidades útiles de aleatoriedad que puede ser extraída
mediante una FFT.
3.- Usar compresión para eliminar
sesgos. Como las técnicas de compresión reversibles
hacen que el resultado tenga la misma cantidad de información
que el original y el resultado es mas pequeño que el original
debe necesariamente ocurrir que el resultado contenga más
uniformidad. Hay que tener en cuenta que esta es una técnica
algo burda ya que la mayoría de los compresores añaden
una cabecera conocida y posiblemente algunas cadenas propias repetitivas
en el resultado comprimido.
Una técnica más interesante
es el uso de funciones fuertes de “mezcla”. Una función
fuerte de mezcla toma 2 o más bits de entrada y produce
una salida donde cada bit es una función compleja no lineal
de cada uno de los bits en la entrada. Como promedio, cambiar
un bit de la entrada produce un cambio en la mitad de los bits
de la salida. Además como la relación no es lineal,
no se garantiza que un bit de la salida en particular cambie al
cambiar uno de los bits de la entrada en particular.
Algunas de las funciones de mezcla más
interesantes son :
Un punto interesante es que las funciones
de mezcla no aumentan la impredecibilidad de los bits presentes
en la entrada. Si introducimos por ejemplo en MD5 cuatro bloques
de 32 bits, cada uno de los cuales tiene 12 bits de entropía
(por ejemplo 4096 valores igualmente probables) el resultado de
MD5 aunque tiene 128 bits de tamaño, solo contiene 48 bits
impredecibles. La salida podrían ser cientos o miles de
bits, mezclando con un contador que vaya dando valores sucesivos
por ejemplo, pero el adversario podría limitarse a buscar
entre 2^48 valores.
Para este uso DES tiene la ventaja de
ser uno de los algoritmos mas testados y documentados; además
existen muchas implementaciones en software y hardware. Los algoritmos
SHS y MD* son bastante más recientes aunque no hay razones
para dudar de su fortaleza. DES, SHS, MD4 y MD5 se pueden usar
sin pagar royalties para cualquier propósito. MD2 se licenció
solo para uso no comercial en conexión con el sistema PEM
(Private Enhanced Mail). Algunos dicen de los MD* que MD2 es fuerte
pero lento, MD4 es rápido pero débil y MD5 estaría
en el justo medio.
Para terminar y resumiendo, podemos obtener
verdaderos números aleatorios si:

